题目内容

3．空间四边形P-ABC中，PA=PB=PC=AB=BC=CA．
（1）写出图中几组异面直线；
（2）画出与AB，PC都垂直且相交的直线．

分析 （1）由已知中空间四边形P-ABC中，PA=PB=PC=AB=BC=CA，可得空间四边形P-ABC是一个正四面体，进而根据正四面体的几何特征，得到三组异面直线；
（2）根据正四面体的几何特征，可得连接PA和BC的中点E，F所得直线EF与AB，PC都垂直且相交．

解答 解：（1）如图所示：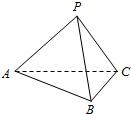

∵PA=PB=PC=AB=BC=CA，
故空间四边形P-ABC是一个正四面体，
则PA与BC异面，PB与AC异面，PC与AB异面；
（2）连接PA和BC的中点E，F，
则由正四面体的几何特征可知：
EF与AB，PC都垂直且相交，
如下图所示：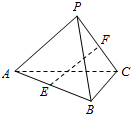

点评 本题考查的知识点是空间中直线与直线之间的位置关系，棱锥的结构特征，熟练掌握正四面体的几何特征是解答的关键．

练习册系列答案
相关题目
13．下列命题中，正确的是④（填写所有正确结论的序号）
①向量$\overrightarrow a$与向量$\overrightarrow b$平行，则$\overrightarrow a$与$\overrightarrow b$的方向相同或相反；
②在△ABC中，点O为平面内一点，若满足$\overrightarrow{OA}•\overrightarrow{OB}=\overrightarrow{OB}•\overrightarrow{OC}=\overrightarrow{OC}•\overrightarrow{OA}$，则点O为△ABC的外心；
③函数$y=tan（2x-\frac{π}{3}）$的对称中心为$（\frac{kπ}{2}+\frac{π}{6}，0），（k∈Z）$
④在△ABC中，若sin（A-B）=1+2cos（B+C）sin（A+C），则△ABC的形状一定是直角三角形．
14．给出以下四个选项，正确的个数是（　　）
①函数f（x）=sin2xcosx的图象关于直线x=π对称
②函数y=3•2x+1的图象可以由函数y=2x的图象仅通过平移得到．
③函数y=$\frac{1}{2}$ln$\frac{1-cosx}{1+cosx}$与y=lntan$\frac{x}{2}$是同一函数．
④在△ABC中，若$\frac{\overrightarrow{AB}•\overrightarrow{BC}}{3}$=$\frac{\overrightarrow{BC}•\overrightarrow{CA}}{2}$=$\frac{\overrightarrow{CA}•\overrightarrow{AB}}{1}$，则tanA：tanB：tanC=3：2：1．
A．1个B．2个C．3个D．0个
11．已知sinα=$\frac{1}{2}$，求$\frac{3cosα+sinα}{2sinα-cosα}$的值．
18．已知cos（α+$\frac{π}{4}$）=$\frac{3}{5}$，$\frac{π}{2}$≤α＜$\frac{3π}{2}$．
（1）求sin（α+$\frac{π}{4}$）的值；
（2）求cos（2α+$\frac{π}{4}$）的值．
8．（重点中学做）如图所示，程序框图输出的某一实数对（x，y）中，若y=1024，则x=（　　）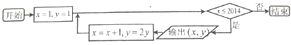
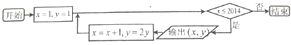
A．9B．10C．11D．12
15．证明；当x＞1时，有ln2（x+1）＞lnx•ln（x+2）
12．已知an=n2，cn=$\frac{1}{{a}_{n}}$，Tn为{cn}的前n项和，求证：1≤Tn＜2．
13．已知A={1，2，x2-5x+9}，B={3，x2+ax+a}，如果A={1，2，3}，2∈B，求实数a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网