题目内容
15.证明;当x>1时,有ln2(x+1)>lnx•ln(x+2)分析 证明:(x+1)2>x2+2x>1,取对数,结合基本不等式,即可证明结论.
解答 证明:∵x>1,
∴(x+1)2>x2+2x>1,
∴ln(x+1)2>ln[x(x+2)]>0,
∴2ln(x+1)>lnx+ln(x+2),
∴ln(x+1)>$\frac{1}{2}$[lnx+ln(x+2)],
∵$\frac{1}{2}$[lnx+ln(x+2)]>$\sqrt{lnx•ln(x+2)}$,
∴ln(x+1)>$\sqrt{lnx•ln(x+2)}$,
∴当x>1时,有ln2(x+1)>lnx•ln(x+2).
点评 本题考查不等式的证明,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知定义在R上的函数f(x)满足f′(x)>1,则不等式f(x)+2x+1>f(3x+1)的解集是( )
| A. | (-∞,-1) | B. | (-1,+∞) | C. | (-∞,-$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,+∞) |
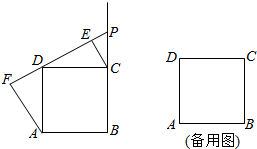 如图,正方形ABCD中,点P是射线BC上的任意一点(点B与点C除外),连接DP,分别过点C,A作直线DP的垂线,垂足为点E,F.
如图,正方形ABCD中,点P是射线BC上的任意一点(点B与点C除外),连接DP,分别过点C,A作直线DP的垂线,垂足为点E,F.