题目内容
(本题满分13分)
把一颗骰子投掷两次，记第一次出现的点数为
，第二次出现的点数为
（其中
）．
（Ⅰ）若记事件
“焦点在
轴上的椭圆的方程为
”，求事件的概率；
（Ⅱ）若记事件
“离心率为2的双曲线的方程为
”，求事件的概率．
把一颗骰子投掷两次，记第一次出现的点数为
，第二次出现的点数为（其中）．（Ⅰ）若记事件
“焦点在轴上的椭圆的方程为”，求事件的概率；（Ⅱ）若记事件
“离心率为2的双曲线的方程为”，求事件的概率．解：
所有可能的情况共有6×6=36种（如下图）
……………4分
（Ⅰ）事件表示“焦点在轴上的椭圆”， 方程
表示焦点在轴上的椭圆，则
，
所以
． …………………………………………9分
（Ⅱ）事件表示“离心率为2的双曲线”，即
，
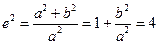所以
，则满足条件的有（1，3），（2，6），因此
．………13
所有可能的情况共有6×6=36种（如下图）| （1，1） | （1，2） | （1，3） | （1，4） | （1，5） | （1，6） |
| （2，1） | （2，2） | （2，3） | （2，4） | （2，5） | （2，6） |
| （3，1） | （3，2） | （3，3） | （3，4） | （3，5） | （3，6） |
| （4，1） | （4，2） | （4，3） | （4，4） | （4，5） | （4，6） |
| （5，1） | （5，2） | （5，3） | （5，4） | （5，5） | （5，6） |
| （6，1） | （6，2） | （6，3） | （6，4） | （6，5） | （6，6） |
……………4分
（Ⅰ）事件
表示“焦点在轴上的椭圆”， 方程表示焦点在轴上的椭圆，则，所以
． …………………………………………9分（Ⅱ）事件
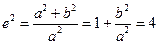表示“离心率为2的双曲线”，即，所以
，则满足条件的有（1，3），（2，6），因此．………13略
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
，则任取
，关于x的方
有实根的概率为
表示抽取的5名学生中考前心理状态好的人数，求P(
，（1）设集合
，分别从集合
和
中随机取一个数为
和
，求函数
在区间
上是增函数的概率；（2）设点
是区域
内的随机点，
，
，
，某次全市20000人参加的考试，数学成绩大致服从正态分布
，则本次考试120分以上的学生约有 人．
的展开系数中x3的系数是 .
的分布列为
，则
_________；
____________。