题目内容
已知向量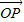
=（2，1），
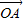=（1，7），
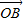=（5，1），设X是直线OP上的一点（O为坐标原点），那么
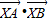的最小值是 ．
【答案】分析：先设出X的坐标，则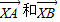
的坐标可得，进而利用平面向量的运算法则求得
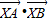的表达式，利用对称轴求得λ，求得最小值．
解答：解：∵X是直线OP上的点，则设X（2λ，λ）
即有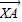
（1-2λ，7-λ），
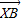（5-2λ，1-λ）
∴
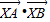=（1-2λ）（5-2λ）+（7-λ）（1-λ）=5-2λ-10λ+4λ2+7-7λ-λ+λ2=5λ2-20λ+12
对称轴为λ=-（-20）÷（5×2）=2
∴最小值为5×2×2-20×2+12=-8
故答案为：-8
点评：本题主要考查了函数的最值及其几何意义．考查了学生对基础知识的综合运用．
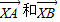的坐标可得，进而利用平面向量的运算法则求得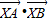的表达式，利用对称轴求得λ，求得最小值．解答：解：∵X是直线OP上的点，则设X（2λ，λ）
即有
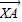（1-2λ，7-λ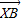），（5-2λ，1-λ）∴
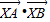=（1-2λ）（5-2λ）+（7-λ）（1-λ）=5-2λ-10λ+4λ2+7-7λ-λ+λ2=5λ2-20λ+12对称轴为λ=-（-20）÷（5×2）=2
∴最小值为5×2×2-20×2+12=-8
故答案为：-8
点评：本题主要考查了函数的最值及其几何意义．考查了学生对基础知识的综合运用．
练习册系列答案
名师点拨卷系列答案
相关题目
已知向量
=（2，1），
•
=10，|
+
|=5
，则|
|=（ ）
| a |
| a |
| b |
| a |
| b |
| 2 |
| b |
A、
| ||
B、
| ||
| C、5 | ||
| D、25 |
已知向量
=（2，1），
=（x，3），且
∥
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
A、
| ||
| B、3 | ||
| C、6 | ||
| D、9 |
已知向量
=（2，-1，3），
=（-4，2，x），且
⊥
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|