题目内容
设f:N*→N*,f(x)是定义在正整数集上的增函数,且f(f(k))=3k,则f(2012)=______.
∵f(f(k))=3k,∴取k=1,得f(f(1))=3,
假设f(1)=1时,有f(f(1))=f(1)=1矛盾
假设f(1)≥3,因为函数是正整数集上的增函数,得f(f(1))≥f(3)>f(1)≥3矛盾
由以上的分析可得:f(1)=2,代入f(f(1))=3,得f(2)=3,
可得f(3)=f(f(2))=3×2=6,f(6)=f(f(3))=3×3=9,f(9)=f(f(6))=3×6=18
由f(f(k))=3k,取k=4和5,得f(f(4))=12,f(f(5))=15,
∵在f(6)和f(9)之间只有f(7)和f(8),且f(4)<f(5),
∴f(4)=7,f(7)=12,f(8)=15,f(5)=8,
由f(x)是增函数可得f(x)的反函数f-1(x)也是增函数
下证f(3k)=3f(k),且f-1(3k)=3f-1(k),
①若f(3k)<3f(k),则f-1(3k)<3f-1(k),
∵满足f(n)=k的n必定满足n<k,即f-1(k)<k,得f-1(3k)<3k
∴3f-1(3k)<9k=f(f(3k))<f(3f(k)),得3f(k)>3f-1(3k),矛盾
②若f(3k)>3f(k),则类似①的证法可得3f(k)<3f-1(3k),矛盾
综上所述,得f(3k)=3f(k)且f-1(3k)=3f-1(k)
∴f(2187)=f(3×729)=3f(729)=32f(243)=33f(81)=34f(27)=35f(9)=36f(3)=37f(1)=4374,
同理f(1944)=35×f(8)=243×15=3645
又∵f(f(k))=3k,∴f(k)的值域包括所有3的倍数.
∵1944到2187间有242个数,3645到4374之间有242个三的倍数,
∴1944到2187之间全部值都是3的倍数
由此可得:f(2012)=3645+(2012-1944)×3=3849
假设f(1)=1时,有f(f(1))=f(1)=1矛盾
假设f(1)≥3,因为函数是正整数集上的增函数,得f(f(1))≥f(3)>f(1)≥3矛盾
由以上的分析可得:f(1)=2,代入f(f(1))=3,得f(2)=3,
可得f(3)=f(f(2))=3×2=6,f(6)=f(f(3))=3×3=9,f(9)=f(f(6))=3×6=18
由f(f(k))=3k,取k=4和5,得f(f(4))=12,f(f(5))=15,
∵在f(6)和f(9)之间只有f(7)和f(8),且f(4)<f(5),
∴f(4)=7,f(7)=12,f(8)=15,f(5)=8,
由f(x)是增函数可得f(x)的反函数f-1(x)也是增函数
下证f(3k)=3f(k),且f-1(3k)=3f-1(k),
①若f(3k)<3f(k),则f-1(3k)<3f-1(k),
∵满足f(n)=k的n必定满足n<k,即f-1(k)<k,得f-1(3k)<3k
∴3f-1(3k)<9k=f(f(3k))<f(3f(k)),得3f(k)>3f-1(3k),矛盾
②若f(3k)>3f(k),则类似①的证法可得3f(k)<3f-1(3k),矛盾
综上所述,得f(3k)=3f(k)且f-1(3k)=3f-1(k)
∴f(2187)=f(3×729)=3f(729)=32f(243)=33f(81)=34f(27)=35f(9)=36f(3)=37f(1)=4374,
同理f(1944)=35×f(8)=243×15=3645
又∵f(f(k))=3k,∴f(k)的值域包括所有3的倍数.
∵1944到2187间有242个数,3645到4374之间有242个三的倍数,
∴1944到2187之间全部值都是3的倍数
由此可得:f(2012)=3645+(2012-1944)×3=3849

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
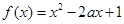 对任意
对任意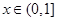 恒有
恒有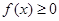 成立,则实数
成立,则实数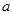 的取值范围是( )
的取值范围是( )