题目内容
求函数y=loga(x-x2)(a>0,a≠1)的定义域、值域、单调区间.
(1)由x-x要使函数有意义,必须,x-x2>0得0<x<1,
所以函数y=loga(x-x2)的定义域是(0,1)(2分)
(2)因为0<x-x2=-(x-
)2+
≤
,
所以,当0<a<1时,loga(x-x2)≥loga
函数y=loga(x-x2)的值域为 [loga
,+∞);(5分)
当a>1时,loga(x-x2)≤loga
函数y=loga(x-x2)的值域为 (-∞,loga
](8分)
(3)当0<a<1时,函数y=loga(x-x2)
在 (0,
]上是减函数,在 [
,1)上是增函数;(10分)
当a>1时,函数y=loga(x-x2)
在 (0,
]上是增函数,在 [
,1)上是减函数.(12分)
所以函数y=loga(x-x2)的定义域是(0,1)(2分)
(2)因为0<x-x2=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
所以,当0<a<1时,loga(x-x2)≥loga
| 1 |
| 4 |
函数y=loga(x-x2)的值域为 [loga
| 1 |
| 4 |
当a>1时,loga(x-x2)≤loga
| 1 |
| 4 |
函数y=loga(x-x2)的值域为 (-∞,loga
| 1 |
| 4 |
(3)当0<a<1时,函数y=loga(x-x2)
在 (0,
| 1 |
| 2 |
| 1 |
| 2 |
当a>1时,函数y=loga(x-x2)
在 (0,
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
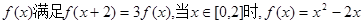 ,则
,则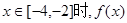 的最小值是 ( )
的最小值是 ( )