题目内容
14.设y=f(x)是定义在实数集R上的函数,且满足f(-x)=f(x)与f(4-x)=f(x),若当x∈[0,2]时,f(x)=-x2+1,则当x∈[-6,-4]时,求f(x)的解析式.分析 由f(-x)=f(x)与f(4-x)=f(x)可得f(x)是周期为4的偶函数,
解答 解:∵f(-x)=f(x),
∴f(4-x)=f(x-4)=f(x),
∴f(x)是周期为4的偶函数.
∵当x∈[0,2]时,f(x)=-x2+1,
∴当x∈[4,6]时,f(x)=-(x-4)2+1,
∵f(x)是偶函数,
∴当x∈[-6,-4]时,f(x)=-(-x-4)2+1=-x2-8x-15.
点评 本题考查了函数奇偶性与周期性的应用,合理构造自变量的对应区间是关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
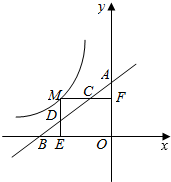 如图,M为曲线y=-$\frac{4}{x}$上的一点.过点M作x轴、y轴的垂线.垂足分别为E、F.分别交直线y=$\frac{\sqrt{3}}{3}$x+m于点D、C两点.若直线y=$\frac{\sqrt{3}}{3}$x+m与y轴交于点A.与x轴相交于点B;
如图,M为曲线y=-$\frac{4}{x}$上的一点.过点M作x轴、y轴的垂线.垂足分别为E、F.分别交直线y=$\frac{\sqrt{3}}{3}$x+m于点D、C两点.若直线y=$\frac{\sqrt{3}}{3}$x+m与y轴交于点A.与x轴相交于点B;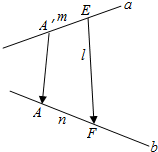 如图,两条异面直线a,b所成的角为θ,在直线a,b上分别取点A′,E和点A,F,使AA′⊥a,且AA′⊥b(AA′称为异面直线a,b的公垂线),已知A′E=m,AF=n,EF=l,求公垂线AA′的长.
如图,两条异面直线a,b所成的角为θ,在直线a,b上分别取点A′,E和点A,F,使AA′⊥a,且AA′⊥b(AA′称为异面直线a,b的公垂线),已知A′E=m,AF=n,EF=l,求公垂线AA′的长.