题目内容
9.证明:tan2α-$\frac{1}{ta{n}^{2}α}$=-$\frac{2sin4α}{si{n}^{3}2α}$.分析 化切为弦,得到tan2α-$\frac{1}{ta{n}^{2}α}$=$\frac{si{n}^{2}α}{co{s}^{2}α}-\frac{co{s}^{2}α}{si{n}^{2}α}$,再通分,利用同角三角函数关系式、二倍角公式能证明tan2α-$\frac{1}{ta{n}^{2}α}$=-$\frac{2sin4α}{si{n}^{3}2α}$.
解答 证明:tan2α-$\frac{1}{ta{n}^{2}α}$=$\frac{si{n}^{2}α}{co{s}^{2}α}-\frac{co{s}^{2}α}{si{n}^{2}α}$=$\frac{si{n}^{4}α-co{s}^{4}α}{si{n}^{2}αco{s}^{2}α}$=$\frac{si{n}^{2}α-co{s}^{2}α}{(\frac{1}{2}sin2α)^{2}}$=-$\frac{cos2α}{\frac{1}{4}si{n}^{2}2α}$=-$\frac{4cos2α}{si{n}^{2}2α}$
-$\frac{2sin4α}{si{n}^{3}2α}$=-$\frac{2×2sin2αcos2α}{si{n}^{3}2α}$=-$\frac{4soc2α}{si{n}^{2}2α}$=-$\frac{2sin4α}{si{n}^{3}2α}$.
∴tan2α-$\frac{1}{ta{n}^{2}α}$=-$\frac{2sin4α}{si{n}^{3}2α}$.
点评 本题考查三角形恒等式的证明,是中档题,解题时要认真审题,注意化切为弦、同角三角函数关系式、二倍角公式的合理运用.

练习册系列答案
相关题目
19.设变量x与y线性相关,且相关系数为0.875,设变量x1=10x,y1=10y,则变量y1与x1的相关系数为( )
| A. | 0.875 | B. | 0.125 | C. | 1 | D. | 不确定 |
18.如图,半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的体积与该圆柱的体积之比是( )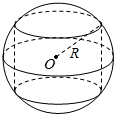

| A. | $\frac{4}{3}$ | B. | $\frac{4\sqrt{2}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
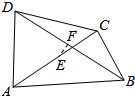 如图,在空间四边形ABCD中,连接AC,BD,E,F分别是边AC.BD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$-2$\overrightarrow{c}$,$\overrightarrow{CD}$=5$\overrightarrow{a}$+6$\overrightarrow{b}$-8$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{EF}$.
如图,在空间四边形ABCD中,连接AC,BD,E,F分别是边AC.BD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$-2$\overrightarrow{c}$,$\overrightarrow{CD}$=5$\overrightarrow{a}$+6$\overrightarrow{b}$-8$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{EF}$.