题目内容
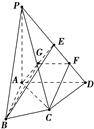
如图,在四棱锥PABCD中,PA⊥底面ABCD,AC⊥CD,∠DAC=60°,AB=BC=AC,E是PD的中点,F为ED的中点.

(1)求证:平面PAC⊥平面PCD;
(2)求证:CF∥平面BAE.

(1)求证:平面PAC⊥平面PCD;
(2)求证:CF∥平面BAE.
见解析
(1)因为PA⊥底面ABCD,所以PA⊥CD,(2分)
又AC⊥CD,且AC∩PA=A,所以CD⊥平面PAC,(4分)
又CD?平面PCD,所以平面PAC⊥平面PCD.(7分)
(2)取AE中点G,连接FG,BG.
因为F为ED的中点,所以FG∥AD且FG=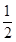 AD.(9分)
AD.(9分)
在△ACD中,AC⊥CD,∠DAC=60°,
所以AC=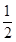 AD,所以BC=
AD,所以BC=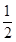 AD.(11分)
AD.(11分)
在△ABC中,AB=BC=AC,所以∠ACB=60°,
从而∠ACB=∠DAC,所以AD∥BC.
综上,FG∥BC,FG=BC,四边形FGBC为平行四边形,所以CF∥BG.(13分)
又BG?平面BAE,CF?平面BAE,所以CF∥平面BAE.(14分)
又AC⊥CD,且AC∩PA=A,所以CD⊥平面PAC,(4分)
又CD?平面PCD,所以平面PAC⊥平面PCD.(7分)
(2)取AE中点G,连接FG,BG.

因为F为ED的中点,所以FG∥AD且FG=
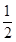 AD.(9分)
AD.(9分)在△ACD中,AC⊥CD,∠DAC=60°,
所以AC=
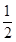 AD,所以BC=
AD,所以BC=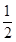 AD.(11分)
AD.(11分)在△ABC中,AB=BC=AC,所以∠ACB=60°,
从而∠ACB=∠DAC,所以AD∥BC.
综上,FG∥BC,FG=BC,四边形FGBC为平行四边形,所以CF∥BG.(13分)
又BG?平面BAE,CF?平面BAE,所以CF∥平面BAE.(14分)

练习册系列答案
相关题目
 .等边三角形ADB以AB为轴转动.
.等边三角形ADB以AB为轴转动.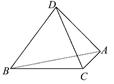
 中
中 ,平面
,平面 外一条线段AB满足AB∥DE,AB
外一条线段AB满足AB∥DE,AB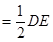 ,AB⊥AC,F是CD的中点.
,AB⊥AC,F是CD的中点.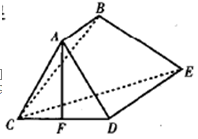
 的底面是正方形,
的底面是正方形, 底面
底面 ,
, 是
是 上一点
上一点
 平面
平面 ;
; ,
, ,求点
,求点 到平面
到平面 的距离.
的距离. 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则能得出
是两个不同的平面,则能得出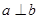 的是( )
的是( ) ,
, ,
,
 ,
,
 ,
,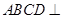 平面
平面 ,四边形
,四边形 是正方形,四边形
是正方形,四边形 ,
,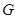 是
是 的中点,则
的中点,则 与平面
与平面 所成角的正弦值为___________.
所成角的正弦值为___________.





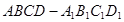 中,点
中,点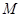 是
是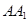 的中点,
的中点,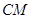 和
和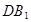 所成角的余弦值为( )
所成角的余弦值为( )


