题目内容
已知抛物线C: 的焦点为F,直线y=2x-4与C交于A,B两点.则cos∠AFB=( )
的焦点为F,直线y=2x-4与C交于A,B两点.则cos∠AFB=( )
A. |
B.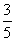 |
C.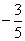 |
D. |
D
解析

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
设双曲线C: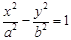 (
(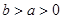 )的左、右焦点分别为 F1,F2.若在双曲线的右支上存在
)的左、右焦点分别为 F1,F2.若在双曲线的右支上存在
一点P,使得 |PF1|=3|PF2|,则双曲线C的离心率e的取值范围为 ( )
| A.(1,2) | B.(1,2] | C.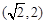 | D.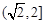 |
已知双曲线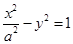 (
(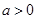 ),与抛物线
),与抛物线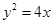 的准线交于
的准线交于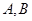 两点,
两点, 为坐标原点,若
为坐标原点,若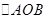 的面积等于
的面积等于 ,则
,则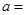
A.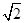 | B. | C.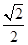 | D.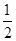 |
已知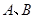 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点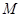 作直线
作直线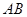 的垂线,垂足为
的垂线,垂足为 .若
.若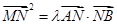 ,其中
,其中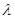 为常数,则动点
为常数,则动点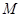 的轨迹不可能是( )
的轨迹不可能是( )
| A.圆 | B.椭圆 | C.抛物线 | D.双曲线 |
已知直线 被双曲线
被双曲线 的两条渐近线所截得线段的长度恰好等于其一个焦点到渐近线的距离,则此双曲线的离心率为( )
的两条渐近线所截得线段的长度恰好等于其一个焦点到渐近线的距离,则此双曲线的离心率为( )
A. | B. | C.2 | D.3 |
若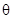 是任意实数,则方程
是任意实数,则方程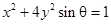 所表示的曲线一定不是( )
所表示的曲线一定不是( )
| A.直线 | B.双曲线 | C.抛物线 | D.圆 |
已知双曲线 的左右焦点分别是
的左右焦点分别是 ,过
,过 的直线
的直线 与双曲线相交于
与双曲线相交于 、
、 两点,则满足
两点,则满足 的直线
的直线 有 ( )
有 ( )
| A.1条 | B.2条 | C.3条 | D.4条 |
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A. | B. |
C. | D. |
已知圆 :
: 和圆
和圆 :
: ,动圆M同时与圆
,动圆M同时与圆 及圆
及圆 相外切,则动圆圆心M的轨迹方程是( ).
相外切,则动圆圆心M的轨迹方程是( ).
A. |
B. |
C. |
D. |