题目内容
3.在直角坐标系xOy中已知点A(1,1),B(3,3),C(4,2).(1)若$\overrightarrow{OQ}$=λ1$\overrightarrow{OC}$+λ2$\overrightarrow{OB}$,(λ1,λ2∈R,且满足λ1+λ2=1.写出Q的轨迹方程(可以只写结果);
(2)点P(x,y)在三角形ABC三边围成的区域内(含边界),若有$\overrightarrow{OP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$(m,n∈R).用x,y表示m+n,并求m+n的取值范围.
分析 (1)设Q(x,y),由$\overrightarrow{OQ}$=λ1$\overrightarrow{OC}$+λ2$\overrightarrow{OB}$,可得(x,y)=λ1(4,2)+λ2(3,3),又λ1+λ2=1.消去λ1,λ2化简即可得出.
(2)$\overrightarrow{AB}$=(2,2),$\overrightarrow{AC}$=(3,1).由$\overrightarrow{OP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,可得(x,y)=m(2,2)+n(3,1).解出可得m+n=$\frac{x+y}{4}$=t,化为y=-x+4t.如图所示,当目标函数与直线BC重合时,t取得最大值,当目标函数经过点A时,t取得最小值,即可得出.
解答 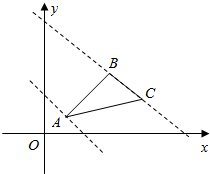 解:(1)设Q(x,y),∵$\overrightarrow{OQ}$=λ1$\overrightarrow{OC}$+λ2$\overrightarrow{OB}$,
解:(1)设Q(x,y),∵$\overrightarrow{OQ}$=λ1$\overrightarrow{OC}$+λ2$\overrightarrow{OB}$,
∴(x,y)=λ1(4,2)+λ2(3,3),
∴$\left\{\begin{array}{l}{x=4{λ}_{1}+3{λ}_{2}}\\{y=2{λ}_{1}+3{λ}_{2}}\end{array}\right.$,又λ1+λ2=1.
化为:x+y=6.即为点Q的轨迹.
(2)$\overrightarrow{AB}$=(2,2),$\overrightarrow{AC}$=(3,1).
∵$\overrightarrow{OP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,∴(x,y)=m(2,2)+n(3,1).
∴$\left\{\begin{array}{l}{x=2m+3n}\\{y=2m+n}\end{array}\right.$,解得n=$\frac{x-y}{2}$,m=$\frac{3y-x}{4}$.
∴m+n=$\frac{x+y}{4}$=t,
化为y=-x+4t.
kBC=$\frac{3-2}{3-4}$=-1.
如图所示,当目标函数与直线BC重合时,t取得最大值,t=$\frac{4+4}{4}$=2.
当目标函数经过点A时,t取得最小值,t=$\frac{1+1}{4}$=$\frac{1}{2}$.
∴m+n的取值范围是$[\frac{1}{2},2]$.
点评 本题考查了向量的线性运算、线性规划、直线方程,考查了推理能力与计算能力,属于中档题.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |