题目内容
(本题满分12分)
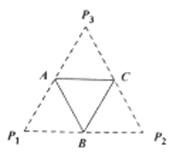
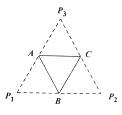
底面边长为2的正三棱锥 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图,求△
,如图,求△ 的各边长及此三棱锥的体积
的各边长及此三棱锥的体积 .
.
边长为4,体积为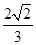 .
.
解析试题分析:由于展开图是 ,
,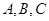 分别是所在边的中点,根据三角形的性质,
分别是所在边的中点,根据三角形的性质, 是正三角形,其边长为4,原三棱锥的侧棱也是2,要求棱锥的体积需要求出棱锥的高,由于是正棱锥,顶点
是正三角形,其边长为4,原三棱锥的侧棱也是2,要求棱锥的体积需要求出棱锥的高,由于是正棱锥,顶点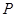 在底面上的射影是底面
在底面上的射影是底面 的中心,由相应的直角三角形可求得高,得到体积.
的中心,由相应的直角三角形可求得高,得到体积.
试题解析:由题意 中
中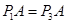 ,
, ,
, ,所以
,所以 是
是 的中位线,因此
的中位线,因此 是正三角形,且边长为4.
是正三角形,且边长为4.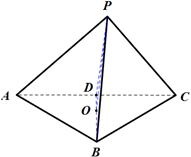
即 ,三棱锥
,三棱锥 是边长为2的正四面体
是边长为2的正四面体
∴如右图所示作图,设顶点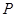 在底面
在底面 内的投影为
内的投影为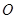 ,连接
,连接 ,并延长交
,并延长交 于
于
∴ 为
为 中点,
中点,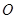 为
为 的重心,
的重心, 底面
底面
∴ ,
,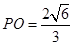 ,
,
【考点】图象的翻折,几何体的体积.

练习册系列答案
相关题目
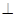 平面PCD;
平面PCD;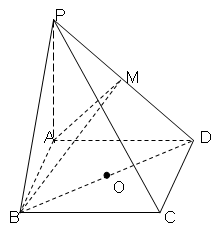
 PD.
PD.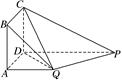
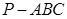 ,其表面展开图是三角形
,其表面展开图是三角形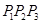 ,如图,求△
,如图,求△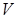 .
.

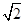 ,求三棱锥D一A1CE的体积.
,求三棱锥D一A1CE的体积. .
.

 求三棱锥B1-A1DC的体积.
求三棱锥B1-A1DC的体积. 内接于球
内接于球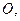

 则
则 两点之间的球面距离
两点之间的球面距离