题目内容
19.在锐角三角形△ABC中,$|\overrightarrow{AB}|=4$,$|\overrightarrow{AC}|=1$,△ABC的面积为$\sqrt{3}$,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
分析 由题设知:△ABC的面积S=$\frac{1}{2}$(|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|×sinA)=2sinA=$\sqrt{3}$,所以sinA=$\frac{\sqrt{3}}{2}$,由此能求出$\overrightarrow{AB}$•$\overrightarrow{AC}$的值.
解答 解:△ABC的面积S=$\frac{1}{2}$(|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|×sinA)=2sinA=$\sqrt{3}$,
∴sinA=$\frac{\sqrt{3}}{2}$,
锐角△ABC中,∠A为锐角,
∴∠A=60°,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|•cosA=4×1×$\frac{1}{2}$=2.
故选:A.
点评 本题考查两个向量的数量积的应用,解题时要认真审题,仔细解答,注意向量在几何中的运用.

练习册系列答案
相关题目
3.已知实数a1,a2,a3,a4,a5构成等比数列,其中a1=2,a5=32,则公比q的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 4 |
7.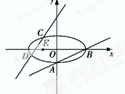 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )| A. | $\frac{7}{6}$ | B. | -$\frac{7}{6}$ | C. | 3 | D. | 6 |
9.设x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x+y-5≥0}\\{2x-y-3≤0}\end{array}\right.$,若使函数Z=ax+by(2b>a>0)的最大值为10,求ab的最大值( )
| A. | $\frac{25}{7}$ | B. | $\frac{5}{7}$ | C. | 5 | D. | 25 |



