题目内容
在数列 和
和 中,已知
中,已知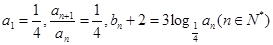 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设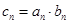 ,求数列
,求数列 的前n项和
的前n项和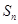 .
.
(1) ,
,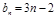 ;(2)
;(2)
解析试题分析:(1)由 可知数列
可知数列 为等比数列,根据等比数列的通项公式求
为等比数列,根据等比数列的通项公式求 ,将
,将 代入
代入 可得
可得 。(2)数列
。(2)数列 的通项公式为等差乘以等比数列所以应用错位相减法求数列的前
的通项公式为等差乘以等比数列所以应用错位相减法求数列的前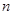 项和。将
项和。将 表示为各项的和,然后将上式两边同时乘以通项公式里边等比数列的公比,但应将第一位空出,然后两式相减即可。
表示为各项的和,然后将上式两边同时乘以通项公式里边等比数列的公比,但应将第一位空出,然后两式相减即可。
试题解析:解:(1)∵
∴数列{ }是首项为
}是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
∴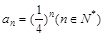 . 4分
. 4分
∵
∴ 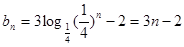 . 6分
. 6分
(2)由(1)知, ,
,  (n
(n )
)
∴ .
.
∴ , ①
, ①
于是 ②
②
8分
① ②得 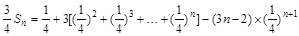
= . 12分
. 12分
∴  . 14分.
. 14分.
考点:1等比数列的定义及通项公式;2错位相减法求数列的和。

练习册系列答案
相关题目
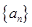 满足
满足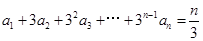 ,
,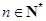 .
.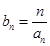 ,求数列
,求数列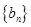 的前
的前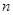 项和
项和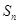 .
. 的前
的前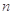 项和
项和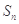 与
与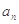 满足
满足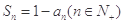 .
. 的前
的前 .
.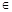 N*,都有
N*,都有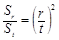 .
.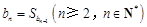 ,求证:数列
,求证:数列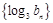 为等比数列;
为等比数列;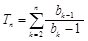 .
. ,都有
,都有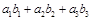
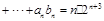 .
. ,试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它
,试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它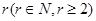 项的和?若存在,请求出该项;若不存在,请说明理由.
项的和?若存在,请求出该项;若不存在,请说明理由. 的前
的前 项和为
项和为 ,且
,且 .
.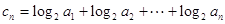 ,
, ,求使
,求使 恒成立的实数
恒成立的实数 的取值范围.
的取值范围.