题目内容
【题目】已知![]() 为定义在
为定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,有
时,有![]() ,且当
,且当![]() 时,
时,![]() ,下列命题正确的是( )
,下列命题正确的是( )
A.![]() B.函数
B.函数![]() 在定义域上是周期为
在定义域上是周期为![]() 的函数
的函数
C.直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点D.函数
个交点D.函数![]() 的值域为
的值域为![]()
【答案】A
【解析】
推导出当![]() 时,
时,![]() ,结合题中等式得出
,结合题中等式得出![]() ,可判断出A选项的正误;利用特殊值法可判断B选项的正误;作出函数
,可判断出A选项的正误;利用特殊值法可判断B选项的正误;作出函数![]() 在区间
在区间![]() 上的图象,利用数形结合思想可判断C选项的正误;求出函数
上的图象,利用数形结合思想可判断C选项的正误;求出函数![]() 在
在![]() 上的值域,利用奇函数的性质可得出函数
上的值域,利用奇函数的性质可得出函数![]() 的值域,可判断出D选项的正误.
的值域,可判断出D选项的正误.
![]() 函数
函数![]() 是
是![]() 上的奇函数,
上的奇函数,![]() ,由题意可得
,由题意可得![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,A选项正确;
,A选项正确;
当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
则函数![]() 不是
不是![]() 上周期为
上周期为![]() 的函数,B选项错误;
的函数,B选项错误;
若![]() 为奇数时,
为奇数时,![]() ,
,
若![]() 为偶数,则
为偶数,则![]() ,即当
,即当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,若
,若![]() ,且当
,且当![]() 时,
时,![]() ,
,
![]() ,
,
当![]() 时,则
时,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,
,
所以,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
由奇函数的性质可知,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
由此可知,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,D选项错误;
,D选项错误;
如下图所示:
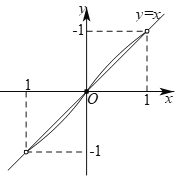
由图象可知,当![]() 时,函数
时,函数![]() 与函数
与函数![]() 的图象只有一个交点,
的图象只有一个交点,
当![]() 或
或![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 与函数
与函数![]() 没有交点,
没有交点,
则函数![]() 与函数
与函数![]() 有且只有一个交点,C选项错误.
有且只有一个交点,C选项错误.
故选:A.

【题目】某饼屋进行为期![]() 天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满
天的五周年店庆活动,现策划两项有奖促销活动,活动一:店庆期间每位顾客一次性消费满![]() 元,可得
元,可得![]() 元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了
元代金券一张;活动二:活动期间每位顾客每天有一次机会获得一个一元或两元红包.根据前一年该店的销售情况,统计了![]() 位顾客一次性消费的金额数(元),频数分布表如下图所示:
位顾客一次性消费的金额数(元),频数分布表如下图所示:
一次性消费金额数 |
|
|
|
|
|
人数 |
|
|
|
|
|
以这![]() 位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
位顾客一次消费金额数的频率分布代替每位顾客一次消费金额数的概率分布.
(1)预计该店每天的客流量为![]() 人次,求这次店庆期间,商家每天送出代金券金额数的期望;
人次,求这次店庆期间,商家每天送出代金券金额数的期望;
(2)假设顾客获得一元或两元红包的可能性相等,商家在店庆活动结束后会公布幸运数字,连续![]() 天参加返红包的顾客,如果红包金额总数与幸运数字一致,则可再获得
天参加返红包的顾客,如果红包金额总数与幸运数字一致,则可再获得![]() 元的“店庆幸运红包”一个.若公布的幸运数字是“
元的“店庆幸运红包”一个.若公布的幸运数字是“![]() ”,求店庆期间一位连续
”,求店庆期间一位连续![]() 天消费的顾客获得红包金额总数的期望.
天消费的顾客获得红包金额总数的期望.
【题目】人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间![]() 内的一个数来表示,该数越接近
内的一个数来表示,该数越接近![]() 表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各
表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各![]() 人进行了调查,调查数据如表所示:
人进行了调查,调查数据如表所示:
幸福感指数 |
|
|
|
|
|
男居民人数 |
|
|
|
|
|
女居民人数 |
|
|
|
|
|
(1)估算该地区居民幸福感指数的平均值;
(2)若居民幸福感指数不小于![]() ,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取
,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取![]() 对夫妻进行调查,用
对夫妻进行调查,用![]() 表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求
表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求![]() 的期望(以样本的频率作为总体的概率).
的期望(以样本的频率作为总体的概率).