题目内容

求证：
11
-
12
-
13
+
14
＜0．
分析：本题中不等式是一个无理数不等式，可采用分析法对其证明，可先把不等式变为
11
+
14
＜
12
+
13
，两边平方寻求不等式成立的条件，直至找到成立的条件
解答：证明：（分析法）
要证
11
-
12
-
13
+
14
＜0，只要证
11
+
14
＜
12
+
13
，（2分）
从而只要证(
11
+
14
)2＜(
12
+
13
)2，即11+2
11×14
+14＜12+2
12×13
+13，
从而只要证
11×14
＜
12×13
，即
154
＜
156
，（2分）
从而只要证(
154
)2＜(
156
)2，即154＜156，而这显然成立．
故
11
-
12
-
13
+
14
＜0．     （2分）
点评：本题考查不等式的证明--分析法，解题的关键是理解并掌握分析法的原理与解题步骤，逐步寻求不等式成立的条件，直至找到已知或公理定理等，分析法是证明不等式的一个重要方法，对于某些条件较少的问题的证明，最是有用
练习册系列答案
相关题目
设A（x1，y1），B（x2，y2）是函数f(x)=
1
2
+log2
x
1-x
的图象上任意两点，且
OM
=
1
2
(
OA
+
OB
)，已知M的横坐标为
1
2
．
（1）求证：M点的纵坐标为定值；
（2）若Sn=
n-1
i=1
f(
i
n
)，其中n∈N*，且n≥2，求Sn；
（3）已知an=
2
3
，n=1
1
(Sn+1)(Sn+1+1)
，n≥2
，其中n∈N*，Tn为数列{an}的前n项和，Tn＜λ（Sn+1+1），对一切n∈N*都成立，试求λ的取值范围．
已知函数f（x）=ax2+ln（x+1）．
（Ⅰ）当a=-
1
4
时，求函数f（x）的单调区间；
（Ⅱ）当x∈[0，+∞）时，不等式f（x）≤x恒成立，求实数a的取值范围．
（Ⅲ）求证：(1+
1
1×2
)(1+
1
2×3
)•…•[1+
1
n(n+1)
]＜e（n∈N*，e是自然对数的底数）．
提示：[ln(x+1)]′=
1
x+1
．
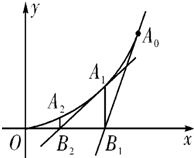精英家教网顶点在坐标原点，开口向上的抛物线经过A0（1，1），过A0作抛物  线的切线交x轴于B1，过B1点作x轴的垂线交抛物线于A1，过A1作抛物线的切线交x轴于B2，…，过An（xn，yn）作抛物线的切线交x轴于Bn+1（xn+1，0）
（1）求{xn}，{yn}的通项公式；
（2）设an=
1
1+xn
+
1
1-xn+1
，数列{an}的前n项和为Tn．求证：Tn＞2n-
1
2
．
（3）设bn=1-log2yn，若对任意正整数n，不等式（1+
1
b1
）（1+
1
b2
）…（1+
1
bn
）≥a
2n+3
成立，求正数a的取值范围．
设f（x）=ln（x+1），（x＞-1）
（1）讨论函数g(x)=af(x)-
1
2
x2（a≥0）的单调性．
（2）求证：(1+
1
1
)(1+
1
2
)(1+
1
3
)…(1+
1
n
)＜e
n+2
2
（n∈N*）
在等差数列{an}中，a1=1，公差d≠0，a22=a1•a4，设数列{22-an}的前n项和为Sn．
（1）解不等式：
Sn-am
Sn+1-am
＜
1
2
，求正整数m，n的值；
（2）若数列{bn}满足b1=4，bn+1=bn2-an•bn+1，求证：
1
1+b1
+
1
1+b2
+…+
1
1+bn
＜
2
5
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网