Question

【题目】已知双曲线C： 的离心率是 ，其一条准线方程为x= ．
（Ⅰ）求双曲线C的方程；
（Ⅱ）设双曲线C的左右焦点分别为A，B，点D为该双曲线右支上一点，直线AD与其左支交于点E，若 =λ ，求实数λ的取值范围．

Answer 1

【答案】解：（I）由题意可得，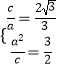
∴a= ，c=2，b=1，
∴双曲线的方程为
（II）由（I）知A（﹣2，0），设D（x0 ， y0），E（x1 ， y1）
则由 =λ ，
可得x1= ，y1= ，
∵E在双曲线上
∴ （ ）2﹣（ ）2=1
（﹣2+λx0）2﹣3（λy0）2=3（1+λ）2
∵D在双曲线
∴可得x0= ，
∴λ≤ ，
∵D在双曲线的左支，点D在右支
∴0＞λ≤
【解析】（I）由题意可得 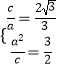，可求a，c，由b2=c2﹣a2可求b，可求双曲线的方程（II）由（I）知A（﹣2，0），设D（x0 ， y0），E（x1 ， y1）则由 =λ ，可得x1= ，y1= ，结合E，D在双曲线上，可求x0 ， 结合双曲线的性质可求λ的取值范围．