题目内容
【题目】已知函数f(x)= ![]() ,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
,函数g(x)=b﹣f(2﹣x),其中b∈R,若函数y=f(x)﹣g(x)恰有4个零点,则b的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞, ![]() )
)
C.(0, ![]() )
)
D.( ![]() ,2)
,2)
【答案】D
【解析】解:∵g(x)=b﹣f(2﹣x), ∴y=f(x)﹣g(x)=f(x)﹣b+f(2﹣x),
由f(x)﹣b+f(2﹣x)=0,得f(x)+f(2﹣x)=b,
设h(x)=f(x)+f(2﹣x),
若x≤0,则﹣x≥0,2﹣x≥2,
则h(x)=f(x)+f(2﹣x)=2+x+x2 ,
若0≤x≤2,则﹣2≤﹣x≤0,0≤2﹣x≤2,
则h(x)=f(x)+f(2﹣x)=2﹣x+2﹣|2﹣x|=2﹣x+2﹣2+x=2,
若x>2,﹣x<﹣2,2﹣x<0,
则h(x)=f(x)+f(2﹣x)=(x﹣2)2+2﹣|2﹣x|=x2﹣5x+8.
即h(x)= 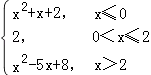 ,
,
作出函数h(x)的图象如图:
当x≤0时,h(x)=2+x+x2=(x+ ![]() )2+
)2+ ![]() ≥
≥ ![]() ,
,
当x>2时,h(x)=x2﹣5x+8=(x﹣ ![]() )2+
)2+ ![]() ≥
≥ ![]() ,
,
故当b= ![]() 时,h(x)=b,有两个交点,
时,h(x)=b,有两个交点,
当b=2时,h(x)=b,有无数个交点,
由图象知要使函数y=f(x)﹣g(x)恰有4个零点,
即h(x)=b恰有4个根,
则满足 ![]() <b<2,
<b<2,
故选:D.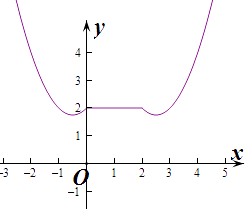
求出函数y=f(x)﹣g(x)的表达式,构造函数h(x)=f(x)+f(2﹣x),作出函数h(x)的图象,利用数形结合进行求解即可.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电x度时,应缴电费y元,写出y关于x的函数关系式;
(2)小明家第一季度缴纳电费情况如表:
月份 | 一月 | 二月 | 三月 | 合计 |
缴费金额 | 82元 | 64元 | 46.8元 | 192.8元 |
问小明家第一季度共用电多少度?