题目内容
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作x轴的垂线交C于点N.(Ⅰ)证明:抛物线C在点N处的切线与AB平行;
(Ⅱ)是否存在实数k使
| NA |
| NB |
分析:(1)设A(x1,2x12),B(x2,2x22),把直线方程代入抛物线方程消去y,根据韦达定理求得x1+x2和x1x2的值,进而求得N和M的横坐标,表示点M的坐标,设抛物线在点N处的切线l的方程将y=2x2代入进而求得m和k的关系,进而可知l∥AB.
(2)假设存在实数k,使
•
=0成立,则可知NA⊥NB,又依据M是AB的中点进而可知|MN|=
|AB|.根据(1)中的条件,分别表示出|MN|和|AB|代入|MN|=
|AB|求得k.
(2)假设存在实数k,使
| NA |
| NB |
| 1 |
| 2 |
| 1 |
| 2 |
解答: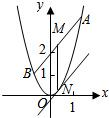 解:(Ⅰ)如图,设A(x1,2x12),B(x2,2x22),
解:(Ⅰ)如图,设A(x1,2x12),B(x2,2x22),
把y=kx+2代入y=2x2得2x2-kx-2=0,
由韦达定理得x1+x2=
,x1x2=-1,
∴xN=xM=
=
,∴N点的坐标为(
,
).
设抛物线在点N处的切线l的方程为y-
=m(x-
),
将y=2x2代入上式得2x2-mx+
-
=0,
∵直线l与抛物线C相切,
∴△=m2-8(
-
)=m2-2mk+k2=(m-k)2=0,
∴m=k,即l∥AB.
(Ⅱ)假设存在实数k,使
•
=0,则NA⊥NB,
又∵M是AB的中点,∴|MN|=
|AB|.
由(Ⅰ)知yM=
(y1+y2)=
(kx1+2+kx2+2)=
[k(x1+x2)+4]=
(
+4)=
+2.
∵MN⊥x轴,
∴|MN|=|yM-yN|=
+2-
=
.
又|AB|=
•|x1-x2|=
•
=
•
=
•
.
∴
=
•
,
解得k=±2.
即存在k=±2,使
•
=0.
 解:(Ⅰ)如图,设A(x1,2x12),B(x2,2x22),
解:(Ⅰ)如图,设A(x1,2x12),B(x2,2x22),把y=kx+2代入y=2x2得2x2-kx-2=0,
由韦达定理得x1+x2=
| k |
| 2 |
∴xN=xM=
| x1+x2 |
| 2 |
| k |
| 4 |
| k |
| 4 |
| k2 |
| 8 |
设抛物线在点N处的切线l的方程为y-
| k2 |
| 8 |
| k |
| 4 |
将y=2x2代入上式得2x2-mx+
| mk |
| 4 |
| k2 |
| 8 |
∵直线l与抛物线C相切,
∴△=m2-8(
| mk |
| 4 |
| k2 |
| 8 |
∴m=k,即l∥AB.
(Ⅱ)假设存在实数k,使
| NA |
| NB |
又∵M是AB的中点,∴|MN|=
| 1 |
| 2 |
由(Ⅰ)知yM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k2 |
| 2 |
| k2 |
| 4 |
∵MN⊥x轴,
∴|MN|=|yM-yN|=
| k2 |
| 4 |
| k2 |
| 8 |
| k2+16 |
| 8 |
又|AB|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
(
|
| 1 |
| 2 |
| k2+1 |
| k2+16 |
∴
| k2+16 |
| 8 |
| 1 |
| 4 |
| k2+1 |
| k2+16 |
解得k=±2.
即存在k=±2,使
| NA |
| NB |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合把握所学知识和基本的运算能力.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
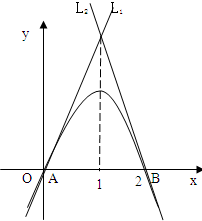 已知抛物线C:y=-x2+2x,在点A(0,0),B(2,0)分别作抛物线的切线L1、L2.
已知抛物线C:y=-x2+2x,在点A(0,0),B(2,0)分别作抛物线的切线L1、L2.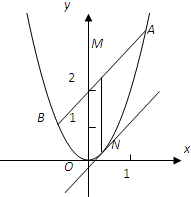 已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.