题目内容

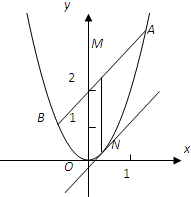已知抛物线C：y=2x2，直线y=kx+2交C于A，B两点，M是线段AB的中点，过M作轴的垂线交C于点N．  
（1）求三角形OAB面积的最小值；
（2）证明：抛物线C在点N处的切线与AB平行；
（3）是否存在实数k使NANB，若存在，求k的值；若不存在，说明理由．
分析：（1）要求三角形OAB面积的最小值，先表示出面积S=
1
2
AB•d（d为O到直线AB的距离），结合函数的性质可求可求
（2）要证明抛物线C在点N处的切线与AB平行，只要证明切线的斜率与直线AB得斜率相等
（法一）：把y=kx+2代入y=2x2得2x2-kx-2=0，由韦达定理可求N点的坐标为(
k
4
，
k2
8
)．可设在点N处的切线l的方程为y-
k2
8
=m(x-
k
4
)，将y=2x2代入整理，由直线l与抛物线C相切，可得△=0
（法二）：把y=kx+2代入y=2x2得2x2-kx-2=0．由韦达定理可求N点坐标，利用导数可求抛物线在点N处的切线l的斜率
（3）（法一）假设存在实数k，使
NA
•
NB
=0，则NA⊥NB，结合已知M是AB的中点，可得|MN|=
1
2
|AB|，结合方程的根与系数的关系及弦长公式代入可求k
（法二）假设存在实数k，使
NA
•
NB
=0结合方程的根与系数的关系代入可求k
解答：解：（1）设A（x1，y1）B（x2，y2），O到直线AB的距离为d=
2
1+k2

联立方程
y=kx+2
y=2x2
整理可得2x2-kx-2=0
则x1+x2=
k
2
，x1x2=-1
∴AB=
(1+k2)[(x1+x2)2-4x1x2
=
(1+k2)(
k2
4
+4)

S△OAB=
1
2
AB•d=
1
2
×
(1+k2)(4+
k2
4
)
×
2
1+k2
=
4+
k2
4
≥2
面积S的最小值为2
解法一：（2）如图，设A（x1，2x12），B（x2，2x22），
把y=kx+2代入y=2x2得2x2-kx-2=0，
由韦达定理得x1+x2=
k
2
，x1x2=-1，xN=xM=
x1+x2
2
=
k
4
，
N点的坐标为(
k
4
，
k2
8
)．
设抛物线在点N处的切线l的方程为y-
k2
8
=m(x-
k
4
)，
将y=2x2代入上式得2x2-mx+
mk
4
-
k2
8
=0，
直线l与抛物线C相切，∴△=m2-8(
mk
4
-
k2
8
)=m2-2mk+k2=(m-k)2=0，
∴m=k．即l∥AB．
（2）假设存在实数k，使
NA
•
NB
=0，则NA⊥NB，又∵M是AB的中点，∴|MN|=
1
2
|AB|．
由（Ⅰ）知yM=
1
2
(y1+y2)=
1
2
(kx1+2+kx2+2)=
1
2
[k(x1+x2)+4]=
1
2
(
k2
2
+4)=
k2
4
+2
∵MN⊥轴，∴|MN|=|yM-yN|=
k2
4
+2-
k2
8
=
k2+16
8
．
又|AB|=
1+k2
•|x1-x2|=
1+k2
•
(x1+x2)2-4x1x2

=
1+k2
•
(
k
2
)2-4×(-1)
=
1
2
k2+1
•
k2+16
．
∴
k2+16
8
=
1
4
k2+1
•
k2+16
，解得k=±2．  
即存在k=±2，使
NA
•
NB
=0．
解法二：（1）如图，设A（x1，2x12），B（x2，2x22），
把y=kx+2代入y=2x2得2x2-kx-2=0．
由韦达定理得x1+x2=
k
2
，x1x2=-1．xN=xM=
x1+x2
2
=
k
4
，
N点的坐标为(
k
4
，
k2
8
)．∵y=2x2，∴y'=4x，
抛物线在点N处的切线l的斜率为4×
k
4
=k，∴l∥AB．
（2）假设存在实数k，使
NA
•
NB
=0．
由（1）知
NA
=(x1-
k
4
，2
x
2
1
-
k2
8
)，
NB
=(x2-
k
4
，2
x
2
2
-
k2
8
)，则
NA
•
NB
=(x1-
k
4
)(x2-
k
4
)+(2
x
2
1
-
k2
8
)(2
x
2
2
-
k2
8
)
=(x1-
k
4
)(x2-
k
4
)+4(
x
2
1
-
k2
16
)(
x
2
2
-
k2
16
)
=(x1-
k
4
)(x2-
k
4
)•[1+4(x1+
k
4
)(x2+
k
4
)]
=[x1x2-
k
4
(x1+x2)+
k2
16
]•[1+4x1x2+k(x1+x2)+
k2
4
]
=(-1-
k
4
×
k
2
+
k2
16
)•[1+4×(-1)+k×
k
2
+
k2
4
]
=(-1-
k2
16
)(-3+
3
4
k2)=0，
∵-1-
k2
16
＜0，∴-3+
3
4
k2=0，解得k=±2．
即存在k=±2，使
NA
•
NB
=0．
点评：本题主要考查了直线与抛物线的位置关系的应用，直线与曲线联立，根据方程的根与系数的关系，这是处理这类问题的最为长用的方法，但圆锥曲线的特点是计算量比较大，要求考试具备较强的运算推理的能力
练习册系列答案
相关题目
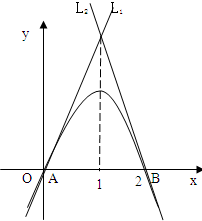精英家教网已知抛物线C：y=-x2+2x，在点A（0，0），B（2，0）分别作抛物线的切线L1、L2．
（1）求切线L1和L2的方程；
（2）求抛物线C与切线L1和L2所围成的面积S．
已知抛物线C：y=x2+4x+
7
2
，过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线．
（1）若抛物线C在点M的法线的斜率为-
1
2
，求点M的坐标（x0，y0）；
（2）设P（-2，4）为C对称轴上的一点，在C上一定存在点，使得C在该点的法线通过点P．试求出这些点，以及C在这些点的法线方程．
已知抛物线C：y=x2，从原点O出发且斜率为k0的直线l0交抛物线C于一异于O点的点A1（x1，y1），过A1作一斜率为k1的直线l1交抛物线C于一异于A1的点A2（x2，y2）…，过An作斜率为kn的直线ln交抛物线C于一异于An的点An+1（xn+1，yn+1）且知kn=k0n+1（k0＞0且k0≠1）．
（1）求x1，x2以及xn与xn+1之间的递推关系式；
（2）求{xn}的通项公式．
（2010•武汉模拟）已知抛物线C：y=
1
2
x2与直线l：y=kx-1没有公共点，设点P为直线l上的动点，过P作抛物线C的两条切线，A，B为切点．
（1）证明：直线AB恒过定点Q；
（2）若点P与（1）中的定点Q的连线交抛物线C于M，N两点，证明：
|PM|
|PN|
=
|QM|
|QN|
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网