题目内容
已知抛物线C:y=x2+4x+| 7 |
| 2 |
(1)若抛物线C在点M的法线的斜率为-
| 1 |
| 2 |
(2)设P(-2,4)为C对称轴上的一点,在C上一定存在点,使得C在该点的法线通过点P.试求出这些点,以及C在这些点的法线方程.
分析:(1)由切线和法线垂直,则其斜率之积等于-1,可得M处的切线的斜率k=2,再根据导数的几何意义,结合已知即可求得点M的坐标;
(2)分x0=-2和x0≠-2两种情况讨论,若x0=-2,则C上点M(-2,-
)处的切线斜率k=0,若x0≠-2,则过点M(x0,y0)的法线方程为:y-y0=-
(x-x0).分别求得法线方程即可.
(2)分x0=-2和x0≠-2两种情况讨论,若x0=-2,则C上点M(-2,-
| 1 |
| 2 |
| 1 |
| 2x0+4 |
解答:解:(1)函数y=x2+4x+
的导数y′=2x+4,点(x0,y0)处切线的斜率k0=2x0+4、
∵过点(x0,y0)的法线斜率为-
,∴-
(2x0+4)=-1,解得x0=-1,y0=
.故点M的坐标为(-1,
).
2设M(x0,y0)3为C上一点,
(2)若x0=-2,则C上点M(-2,-
)处的切线斜率k=0,
过点M(-2,-
)的法线方程为x=-2,法线过点P(-2,4);
若x0≠-2,则过点M(x0,y0)的法线方程为:y-y0=-
(x-x0).
若法线过点P(-2,4),则4-y0=-
(-2-x0),
解得x0=0,y0=
,得x+4y-14=0,或者x0=-4,y0=
,得x-4y+18=0.
综上,在C上有点(0,
),(-4,
)及(-2,-
),
在该点的法线通过点P,法线方程分别为x+4y-14=0,x-4y+18=0,x=-2
| 7 |
| 2 |
∵过点(x0,y0)的法线斜率为-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
2设M(x0,y0)3为C上一点,
(2)若x0=-2,则C上点M(-2,-
| 1 |
| 2 |
过点M(-2,-
| 1 |
| 2 |
若x0≠-2,则过点M(x0,y0)的法线方程为:y-y0=-
| 1 |
| 2x0+4 |
若法线过点P(-2,4),则4-y0=-
| 1 |
| 2x0+4 |
解得x0=0,y0=
| 7 |
| 2 |
| 7 |
| 2 |
综上,在C上有点(0,
| 7 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
在该点的法线通过点P,法线方程分别为x+4y-14=0,x-4y+18=0,x=-2
点评:本题通过曲线的切线和法线问题,考查了导数的运算和几何意义,同时综合运用了分类讨论的数学思想,难度较大.

练习册系列答案
相关题目
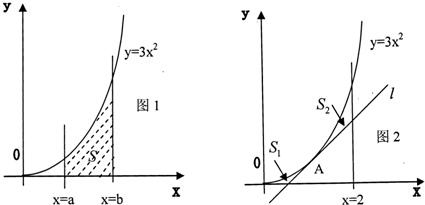
 )2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
)2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.