题目内容
【题目】已知函数f（x）=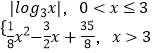 
，若函数g（x）=f（x）﹣m存在4个不同的零点x1 ， x2 ， x3 ， x4 ， 则实数m的取值范围是 ， x1x2x3x4的取值范围是 ．
【答案】（0，1）；（27，35）
【解析】解：作出f（x）的函数图象如图所示：
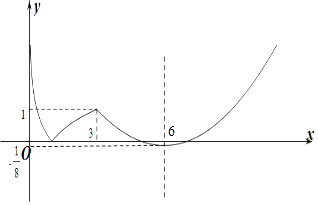
由图象可知当0＜m＜1时，方程f（x）=m有4个解，
设g（x）的4个零点从小到大为x1＜x2＜x3＜x4，
则x1x2=1，x3+x4=12，且3＜x3＜5，
∴x1x2x3x4=x3x4=x3（12﹣x3）=﹣x32+12x3，
设h（x）=﹣x2+12x，x∈（3，5），则h（x）在（3，5）上单调递增，
又h（3）=27，h（5）=35，
∴27＜h（x）＜35．
即27＜x1x2x3x4＜35．
所以答案是：（0，1），（27，35）．
练习册系列答案
精英口算卡系列答案
相关题目
