题目内容
(12分)已知圆C1: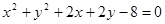 与圆C2:
与圆C2: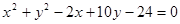 相交于A、B两点。
相交于A、B两点。
⑴ 求公共弦AB的长;
⑵ 求圆心在直线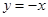 上,且过A、B两点的圆的方程;
上,且过A、B两点的圆的方程;
⑶ 求经过A、B两点且面积最小的圆的方程。
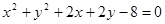 与圆C2:
与圆C2: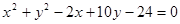 相交于A、B两点。
相交于A、B两点。⑴ 求公共弦AB的长;
⑵ 求圆心在直线
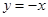 上,且过A、B两点的圆的方程;
上,且过A、B两点的圆的方程;⑶ 求经过A、B两点且面积最小的圆的方程。
⑴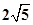 ⑵
⑵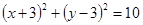 ⑶
⑶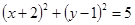
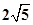 ⑵
⑵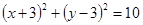 ⑶
⑶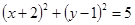
试题分析:⑴由两圆方程相减即得
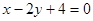
此为公共弦AB所在的直线方程
圆心
 半径
半径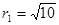
C1到直线AB的距离为
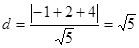
故公共弦长
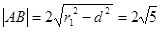
⑵ 圆心
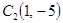 ,过C1,C2的直线方程为
,过C1,C2的直线方程为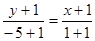 ,即
,即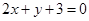
由
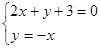 得所求圆的圆心为
得所求圆的圆心为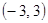
它到AB的距离为
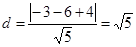
∴所求圆的半径为
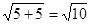
∴所求圆的方程为
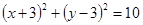
⑶ 过A、B且面积最小的圆就是以AB为直径的圆
由
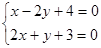 ,得圆心
,得圆心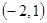 半径
半径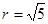
∴所求圆的方程为
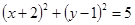
点评:直线与圆相交时圆的半径,圆心到直线的距离,弦长的一半构成直角三角形,第一问主要利用此三角形求解;第二问还可用待定系数法求方程

练习册系列答案
相关题目
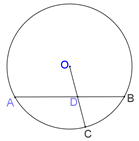
 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、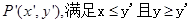 ,则称P优于
,则称P优于 ,如果
,如果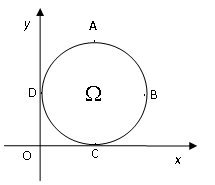
 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求: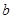 的取值范围;
的取值范围; 与圆C2:
与圆C2: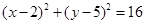 的位置关系是( )
的位置关系是( )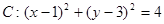 ,过原点
,过原点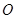 的直线
的直线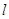 与圆
与圆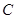 相交于
相交于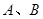 两点
两点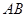 的长为
的长为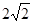 ,求直线
,求直线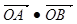 为定值。
为定值。 表示一个圆,则有( )
表示一个圆,则有( )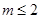

 |PD|.
|PD|.