题目内容
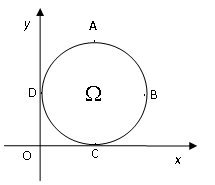
如图,在平面直角坐标系中,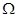 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、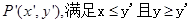 ,则称P优于
,则称P优于 ,如果
,如果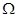 中的点Q满足:不存在
中的点Q满足:不存在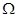 中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( )
中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( )
A. A B.B C. C D.D
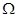 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、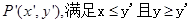 ,则称P优于
,则称P优于 ,如果
,如果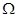 中的点Q满足:不存在
中的点Q满足:不存在 中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( )
中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( )
A. A B.B C. C D.D
D
试题分析:依题意,在点Q组成的集合中任取一点,过该点分别作平行于两坐标轴的直线,构成的左上方区域(权且称为“第二象限”)与点Q组成的集合无公共元素,这样点Q组成的集合才为所求. 检验得:D.
点评:本题考查如何把代数语言翻译成几何语言,即数与形的结合.

练习册系列答案
相关题目
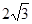 ,连接OC,CD⊥OC交⊙O于D,则CD的最大值为_____________.
,连接OC,CD⊥OC交⊙O于D,则CD的最大值为_____________.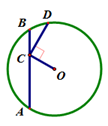
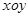 中,已知圆
中,已知圆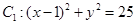 和圆
和圆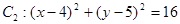 .
.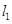 经过点
经过点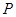 (2,-1)和圆
(2,-1)和圆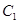 的圆心,求直线
的圆心,求直线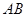 的中点,求直线
的中点,求直线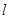 过点
过点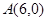 ,且被圆
,且被圆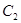 截得的弦长为
截得的弦长为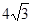 ,求直线
,求直线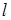 的方程.
的方程. 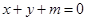 与圆
与圆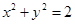 交于不同的两点A、B,O是坐标原点,且
交于不同的两点A、B,O是坐标原点,且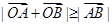 ,则实数m的取值范围是 。
,则实数m的取值范围是 。 上的点到直线
上的点到直线 距离的最大值是( )
距离的最大值是( ) 
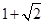


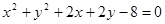 与圆C2:
与圆C2: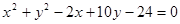 相交于A、B两点。
相交于A、B两点。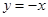 上,且过A、B两点的圆的方程;
上,且过A、B两点的圆的方程; 和
和 为直径端点的圆的方程是
为直径端点的圆的方程是


