题目内容
已知定点A(1,0),B(-1,0),C(0,1),D(0,2),动点P满足: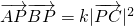 .
.
(1)求动点P轨迹M的方程,并说明方程表示的曲线类型;
(2)当k=2时:
①E是x轴上的动点,EK,EQ分别切曲线M于K,Q两点,如果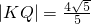 ,求线段KQ的垂直平分线方程;
,求线段KQ的垂直平分线方程;
②若E点在△ABC边上运动,EK,EQ分别切曲线M于K,Q两点,求四边形DKEQ的面积的取值范围.
 解:(1)设动点坐标为P(x,y),
解:(1)设动点坐标为P(x,y),则
 =(x-1,y),
=(x-1,y), =(x+1,y),
=(x+1,y), =(x,1-y);
=(x,1-y);因为
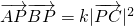 ,所以x2+y2-1=K[x2+(y-1)2];
,所以x2+y2-1=K[x2+(y-1)2];整理得:(k-1)x2+(k-1)y2+k+1=0;
若k=1,则方程为y=1,表示过点(0,1)且平行与x轴的直线,
若k≠1,则方程化为x2+(y-
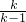 )2=(
)2=( )2,表示以(0,
)2,表示以(0,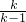 )为圆心,|
)为圆心,| |为半径的圆.
|为半径的圆.(2)①因为k=2,所以方程为x2+(y-2)2=1,圆心为D,如图,
由|KQ|=
 可得|DN|=
可得|DN|= ,
,由射影定理可得|DQ|2=|DN||DE,得|DE|=
 ,
,在Rt△DOE中,|OE|=1,得E(1,0)(-1,0),
ED⊥KQ且平分KQ,所以DE的方程为2x+y-2=0或2x-y+1=0(0<y<1);
②LBC:x+y-1=0(0<y<1),LAC:x-y+1=0(0<y<1),
当E(a,b)在线段AC上运动时,
SDKEQ=2S△DKE=DK•KE=
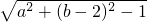 =
=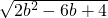 (0<b<1),
(0<b<1),所以0<SDKEQ<2,
同理,当E(a,b)在线段BC上运动时,0<SDKEQ<2
当E(a,b)在线段BC上运动时,E(a,0)(-1≤a≤1),
SDKEQ=2S△DKE=DK•KE=
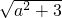 (-1≤a≤1),
(-1≤a≤1),所以
 ≤SDKEQ≤2,
≤SDKEQ≤2,综上可得,0≤SDKEQ≤2.
分析:(1)根据题意,设出P的坐标(x,y);可得则
 、
、 、
、 的坐标,代入
的坐标,代入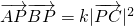 中,可得(k-1)x2+(k-1)y2+k+1=0;分K=1与k≠1两种情况讨论,可得答案.
中,可得(k-1)x2+(k-1)y2+k+1=0;分K=1与k≠1两种情况讨论,可得答案.(2)①根据题意k=2,代入(1)的方程可得x2+(y-2)2=1,进而|DN|=
 ,结合射影定理计算可得|DE|=
,结合射影定理计算可得|DE|= ,在Rt△DOE中,由|OE|=1,得E的坐标,又由ED⊥KQ且平分KQ,由直线的点斜式方程可得答案;
,在Rt△DOE中,由|OE|=1,得E的坐标,又由ED⊥KQ且平分KQ,由直线的点斜式方程可得答案;②由(1)可得线段BC、AC的方程,按E的在△ABC的三边上不同位置,不同分3种情况讨论;求出SDKEQ的范围,综合可得答案.
点评:本题考查直线与圆的方程的综合运用,是解析几何中典型题目,有一定的难度;解题时,要注意不能遗漏对特殊情况的讨论,如本题(1)中对k=1的讨论.

练习册系列答案
相关题目
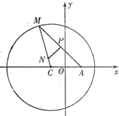 如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足
如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足