题目内容
如图,在正三棱柱ABC-A1B1C1中,AB=2.若二面角C-AB-C1的大小为60°,则异面直线A1B1和BC1所成角的余弦值为
A. | B. | C. | D. |
D
解析试题分析:如图所示,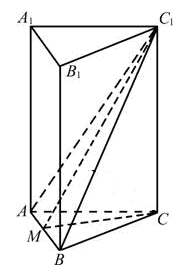
取AB中点M,由C1A=C1B知C1M⊥AB,CM⊥AB,则∠C1MC为二面角C-AB-C1的平面角,在Rt△C1CM中,cos60°=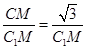 ,∴C1M=2
,∴C1M=2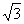 ,∵AB∥
,∵AB∥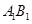 ,∴∠C1BM为所求的异面直线夹角,Rt△C1MB中,tan∠C1BM=
,∴∠C1BM为所求的异面直线夹角,Rt△C1MB中,tan∠C1BM=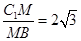 ,∴cos∠C1BM=
,∴cos∠C1BM=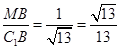 即异面直线A1B1和BC1所成角的余弦值为
即异面直线A1B1和BC1所成角的余弦值为 ,故选D
,故选D
考点:本题考查了异面直线夹角的求法
点评:利用异面直线夹角的概念是解决此类问题的常用方法,属基础题

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
设、 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若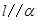 , , ,则 ,则 | D.若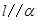 , , ,则 ,则 |
设 是平面
是平面 内的一条定直线,
内的一条定直线, 是平面
是平面 外的一个定点,动直线
外的一个定点,动直线 经过点
经过点 且与
且与 成
成 角,则直线
角,则直线 与平面
与平面 的交点
的交点 的轨迹是
的轨迹是
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
在三棱锥 中,
中, ,
, 是等腰直角三角形,
是等腰直角三角形,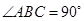 ,
, 为
为 中点. 则
中点. 则 与平面
与平面 所成的角等于( )
所成的角等于( )
A. | B. | C. | D. |
将正方体的纸盒展开如图,直线 、
、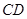 在原正方体的位置关系是( )
在原正方体的位置关系是( )
| A.平行 | B.垂直 | C.相交成60°角 | D.异面且成60°角 |
 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为 的正方形,底面中心为
的正方形,底面中心为 ,以
,以 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )



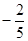
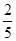
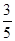
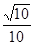
 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,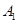 在底面
在底面 上的射影为
上的射影为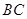 的中点D,则异面直线AD与
的中点D,则异面直线AD与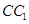 所成的角的余弦值为( )
所成的角的余弦值为( )

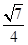
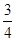
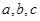 ,若
,若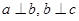 ,则
,则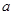 ∥
∥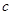 ;②
;②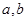 是异面直线,
是异面直线,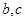 是异面直线,则
是异面直线,则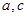 不一定是异面直线;③过空间任一点,有且仅有一条直线和已知平面
不一定是异面直线;③过空间任一点,有且仅有一条直线和已知平面 垂直;④平面
垂直;④平面 ,点
,点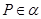 ,直线
,直线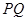 //
//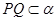 ;其中正确的命题的个数有( )
;其中正确的命题的个数有( )