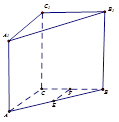
题目内容
在棱长为1的正方体ABCD—A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是 ( )
A.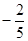 | B.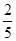 | C.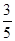 | D.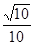 |
B
解析试题分析:先通过平移将两条异面直线平移到同一个起点B1,得到的锐角或直角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可.解:如图,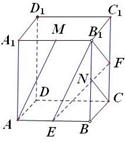
将AM平移到B1E,NC平移到B1F,则∠EB1F为直线AM与CN所成角,设边长为2,则B1E=B1F=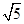 , EF=
, EF=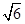 ,∴cos∠EB1F=
,∴cos∠EB1F=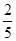 ,故答案为B
,故答案为B
考点:异面直线所成的角
点评:本小题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
设 为两条直线,
为两条直线, 为两个平面,下列说法正确的是( )
为两个平面,下列说法正确的是( )
A.若 ,则 ,则 |
B.若  |
C. |
D.若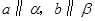 , , ,则 ,则 |
点 到直线
到直线 的距离为( )
的距离为( )
| A.2 | B.1 | C. | D. |
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( )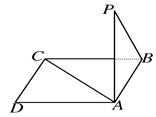
| A.90° | B.60° |
| C.45° | D.30° |
关于直线 、
、 与平面
与平面 、
、 ,有下列四个命题:
,有下列四个命题:
① 且
且 ,则
,则 ; ②
; ② 且
且 ,则
,则 ;
;
③ 且
且 ,则
,则 ; ④
; ④ 且
且 ,则
,则 .
.
其中假命题的序号是:( )
| A.①、② | B.③、④ | C.②、③ | D.①、④ |
单位正方体在一个平面内的投影面积的最大值和最小值分别为( )
A.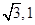 | B.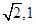 | C.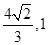 | D.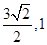 |
如图,正四棱锥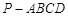 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )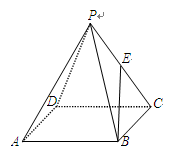
A.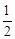 | B.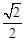 |
C.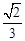 | D.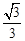 |
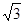 ,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).
,E,F分别为AB、CB中点,过直线EF作棱柱的截面,若截面与平面ABC所成的二面角的大小为60º,则截面的面积为( ).