题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() )的左,右顶点分别为
)的左,右顶点分别为![]() ,
,![]() ,长轴长为
,长轴长为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为椭圆
为椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,证明:直线
的任意一点,证明:直线![]() ,
,![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(3)已知两条互相垂直的直线![]() ,
,![]() 都经过椭圆
都经过椭圆![]() 的右焦点
的右焦点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() 四点,求四边形
四点,求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]() (2)定值
(2)定值![]() ,证明见解析;(3)
,证明见解析;(3)![]()
【解析】
(1)由长轴长为4可求![]() ,再由待定系数法把点代入椭圆方程即可求椭圆的标准方程;
,再由待定系数法把点代入椭圆方程即可求椭圆的标准方程;
(2)设点![]() ,
,![]() ,点
,点![]() 在椭圆上可得
在椭圆上可得![]()
代入上式化简即可.
(3)当![]() ,
,![]() 中有一条斜率不存在时,
中有一条斜率不存在时,![]() ;
;
当![]() ,
,![]() 的斜率都存在时,设过点
的斜率都存在时,设过点![]() 的两条互相垂直的直线
的两条互相垂直的直线![]() :
:![]() ,直线
,直线![]() :
:![]() ,联立
,联立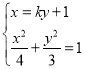 求出
求出![]() 与
与![]() ,所以
,所以![]() 代入整理成关于
代入整理成关于![]() 的式子,求式子的值域即可.
的式子,求式子的值域即可.
解:(1)由题意知: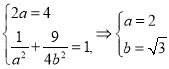 ,
,
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由已知![]() ,
,![]() ,设点
,设点![]() ,则
,则
![]() ,又
,又![]() 在椭圆上,
在椭圆上,![]()
即![]() ,
,
![]()
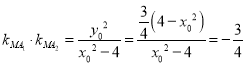 (定值).
(定值).
(3)当![]() ,
,![]() 中有一条斜率不存在时,易求得
中有一条斜率不存在时,易求得![]() ;
;
当![]() ,
,![]() 的斜率都存在时,设过点
的斜率都存在时,设过点![]() 的两条互相垂直的直线
的两条互相垂直的直线![]() :
:![]() ,直线
,直线![]() :
:![]()
由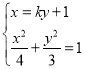 得
得![]()
显然![]() ,
,![]()
![]() ,
,![]()
则![]()
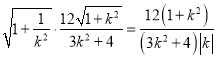 .
.
把上式中的![]() 换成
换成![]() 得:
得:![]()
则四边形![]() 的面积为
的面积为
![]()
![]()
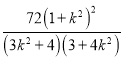
令![]() ,则
,则![]() ,且
,且![]() ,
,![]()
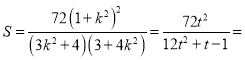
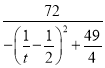
![]() ,
,
![]()
![]() ,
,
所以四边形![]() 的面积的取值范围是
的面积的取值范围是![]() .
.

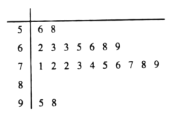
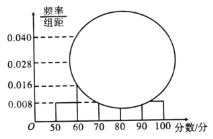
【题目】当前,以“立德树人”为目标的课程改革正在有序推进.高中联招对初三毕业学生进行体育测试,是激发学生、家长和学校积极开展体育活动,保证学生健康成长的有效措施.程度2019年初中毕业生升学体育考试规定,考生必须参加立定跳远、掷实心球、1分钟跳绳三项测试,三项考试满分50分,其中立定跳远15分,掷实心球15分,1分钟跳绳20分.某学校在初三上期开始时要掌握全年级学生每分钟跳绳的情况,随机抽取了100名学生进行测试,得到下边频率分布直方图,且规定计分规则如下表:
每分钟跳绳个数 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
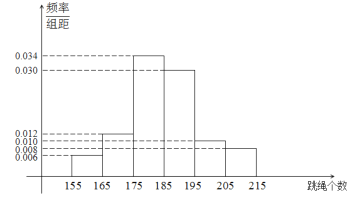
(1)请估计学生的跳绳个数的众数、中位数和平均数(保留整数);
(2)若从跳绳个数在![]() 、
、![]() 两组中按分层抽样的方法抽取9人参加正式测试,并从中任意选取2人,求两人得分之和不大于34分的概率.
两组中按分层抽样的方法抽取9人参加正式测试,并从中任意选取2人,求两人得分之和不大于34分的概率.