题目内容
已知正三棱锥P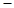 ABC中,E,F分别是AC,PC的中点,若EF
ABC中,E,F分别是AC,PC的中点,若EF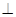 BF,AB=2,则三棱锥P
BF,AB=2,则三棱锥P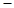 ABC的外接球的表面积为_________.
ABC的外接球的表面积为_________.
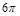
解析试题分析:E,F分别是AC,PC的中点,∴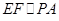 ,∵三棱锥P
,∵三棱锥P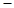 ABC为正棱锥,∴
ABC为正棱锥,∴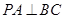 (对棱互相垂直),∴
(对棱互相垂直),∴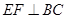 ,又∵EF
,又∵EF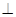 BF,而
BF,而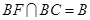 ,∴
,∴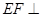 平面
平面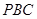 ,∴
,∴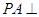 平面
平面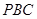 ,∴
,∴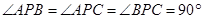 ,以
,以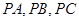 为从同一定点
为从同一定点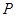 出发的正方体三条棱,将此三棱锥补成以正方体,则它们有相同的外接球,正方体的对角线就是球的直径.又因为AB=2,所以
出发的正方体三条棱,将此三棱锥补成以正方体,则它们有相同的外接球,正方体的对角线就是球的直径.又因为AB=2,所以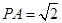 ,∴
,∴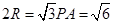 ,∴
,∴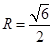 ,∴三棱锥P
,∴三棱锥P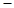 ABC的外接球的表面积为
ABC的外接球的表面积为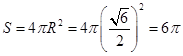 .故答案为:
.故答案为: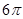 .
.
考点:球内接多面体;球的体积和表面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
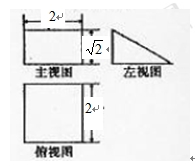
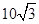 ,则h________.
,则h________.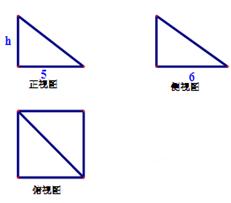
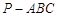 的四个顶点都在球
的四个顶点都在球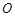 的球面上,若
的球面上,若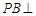 平面
平面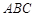 ,
,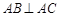 ,且
,且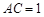 ,
,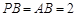 ,则球
,则球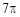
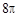
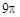
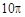
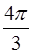 ,则圆锥的体积是________
,则圆锥的体积是________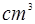 .
.
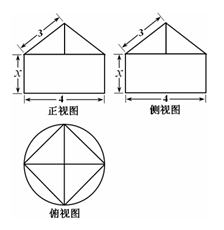
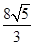 ,则图中x的值为________.
,则图中x的值为________.