题目内容
正方体的内切球,与各棱相切的球,外接球的体积之比为( )
| A.1:2:3 | B. | C. | D. |
C
试题分析:设正方体的棱长为
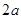 ,则它的内切球半径为
,则它的内切球半径为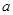 ,与各棱相切的球半径为
,与各棱相切的球半径为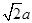 ,外接球的半径为
,外接球的半径为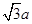 ,所以它们的体积比为
,所以它们的体积比为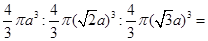
 .
.点评:正方体的内切球的直径等于正方体的棱长,与各棱相切的球的直径等于正方体的面对角线,外接球的直径等于正方体的体对角线.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
题目内容
| A.1:2:3 | B. | C. | D. |
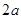 ,则它的内切球半径为
,则它的内切球半径为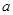 ,与各棱相切的球半径为
,与各棱相切的球半径为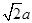 ,外接球的半径为
,外接球的半径为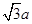 ,所以它们的体积比为
,所以它们的体积比为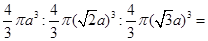
 .
.
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案