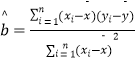题目内容
【题目】设函数f(x)=|x+ ![]() |+|x﹣a|(a>0).
|+|x﹣a|(a>0).
(1)证明:f(x)≥2;
(2)若f(3)<5,求a的取值范围.
【答案】
(1)解:证明:∵a>0,f(x)=|x+ ![]() |+|x﹣a|≥|(x+
|+|x﹣a|≥|(x+ ![]() )﹣(x﹣a)|=|a+
)﹣(x﹣a)|=|a+ ![]() |=a+
|=a+ ![]() ≥2
≥2 ![]() =2,
=2,
故不等式f(x)≥2成立.
(2)解:∵f(3)=|3+ ![]() |+|3﹣a|<5,
|+|3﹣a|<5,
∴当a>3时,不等式即a+ ![]() <5,即a2﹣5a+1<0,解得3<a<
<5,即a2﹣5a+1<0,解得3<a< ![]() .
.
当0<a≤3时,不等式即 6﹣a+ ![]() <5,即 a2﹣a﹣1>0,求得
<5,即 a2﹣a﹣1>0,求得 ![]() <a≤3.
<a≤3.
综上可得,a的取值范围( ![]() ,
, ![]() )
)
【解析】(1)由a>0,f(x)=|x+ ![]() |+|x﹣a|,利用绝对值三角不等式、基本不等式证得f(x)≥2成立.(2)由f(3)=|3+
|+|x﹣a|,利用绝对值三角不等式、基本不等式证得f(x)≥2成立.(2)由f(3)=|3+ ![]() |+|3﹣a|<5,分当a>3时和当0<a≤3时两种情况,分别去掉绝对值,求得不等式的解集,再取并集,即得所求.
|+|3﹣a|<5,分当a>3时和当0<a≤3时两种情况,分别去掉绝对值,求得不等式的解集,再取并集,即得所求.

【题目】某水仙花经营部每天的房租、水电、人工等固定成本为1000元,每盆水仙花的进价是10元,销售单价![]() (元) (
(元) (![]() )与日均销售量
)与日均销售量![]() (盆)的关系如下表,并保证经营部每天盈利.
(盆)的关系如下表,并保证经营部每天盈利.
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
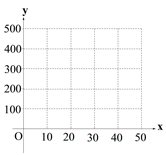
(Ⅰ) 在所给的坐标图纸中,根据表中提供的数据,描出实数对![]() 的对应点,并确定
的对应点,并确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(Ⅱ)求出![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(Ⅲ)请写出该经营部的日销售利润![]() 的表达式,并回答该经营部怎样定价才能获最大日销售利润?
的表达式,并回答该经营部怎样定价才能获最大日销售利润?
【题目】某高级中学今年高一年级招收“国际班”学生![]() 人,学校为这些学生开辟了直升海外一流大学的绿色通道,为了逐步提高这些学生与国际教育接轨的能力,将这
人,学校为这些学生开辟了直升海外一流大学的绿色通道,为了逐步提高这些学生与国际教育接轨的能力,将这![]() 人分为三个批次参加国际教育研修培训,在这三个批次的学生中男、女学生人数如下表:
人分为三个批次参加国际教育研修培训,在这三个批次的学生中男、女学生人数如下表:
第一批次 | 第二批次 | 第三批次 | |
女 |
|
|
|
男 |
|
|
|
已知在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名,抽到第一批次、第二批次中女学生的概率分别是
名,抽到第一批次、第二批次中女学生的概率分别是![]() .
.
(1)求![]() 的值;
的值;
(2)为了检验研修的效果,现从三个批次中按分层抽样的方法抽取![]() 名同学问卷调查,则三个批次被选取的人数分别是多少?
名同学问卷调查,则三个批次被选取的人数分别是多少?
(3)若从第(2)小问选取的学生中随机选出两名学生进行访谈,求“参加访谈的两名同学至少有一个人来自第一批次”的概率.