题目内容
1.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象的相邻两条对称轴的距离是$\frac{π}{2}$,当x=$\frac{π}{6}$时取得最大值2.(1)求函数f(x)的解析式;
(2)若函数g(x)=f(x)-$\frac{6}{5}$的零点为x0,求$cos({\frac{π}{3}-2{x_0}})$.
分析 (1)由已知求出函数的振幅,周期和初相,可得函数f(x)的解析式;
(2)若函数g(x)=f(x)-$\frac{6}{5}$的零点为x0,$f({x_0})=\frac{6}{5}$,利用诱导公式,可得答案.
解答 解:(1)由题意知,振幅A=2,
周期T=$\frac{2π}{ω}=2×\frac{π}{2}$,
∴ω=2,
∴f(x)=2sin(2x+φ).
将点$({\frac{π}{6},2})$代入得:$2sin({\frac{π}{3}+φ})=2⇒sin({\frac{π}{3}+φ})=1$,又$|φ|<\frac{π}{2}$,
故$φ=\frac{π}{6}$.
∴$f(x)=2sin({2x+\frac{π}{6}})$.
(2)由函数$g(x)=f(x)-\frac{6}{5}$的零点为x0知:x0是方程$f(x)=\frac{6}{5}$的根,故$f({x_0})=\frac{6}{5}$,
得sin(2x0+$\frac{π}{6}$)=$\frac{3}{5}$,又(2x0+$\frac{π}{6}$)+($\frac{π}{3}$-2x0)=$\frac{π}{2}$,
∴$cos({\frac{π}{3}-2{x_0}})=cos[{\frac{π}{2}-({2{x_0}+\frac{π}{6}})}]=sin({2{x_0}+\frac{π}{6}})=\frac{3}{5}$.
点评 本题考查的知识点是正弦型函数的图象和性质,熟练掌握正弦型函数的图象和性质,是解答的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
12.(理)现有11个保送大学的名额分配给8个班级,每班至少有1个名额,则名额分配的方法共有( )
| A. | 56种 | B. | 112种 | C. | 120种 | D. | 240种 |
6.已知a>0,b>0,且a+b=ab,则a+$\frac{b}{4}$的最小值为( )
| A. | 1 | B. | $\frac{7}{4}$ | C. | 2 | D. | $\frac{9}{4}$ |
13.设f(sinx)=cos2x,则f($\frac{1}{4}$)=( )
| A. | $-\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | $-\frac{1}{8}$ | D. | $\frac{1}{8}$ |
10.某市欲为市辖各学校招聘教师,从报名者中筛选1000名参加笔试,按笔试成绩择优取200名面试,再从面试对象中聘用100名教师.
(1)随机调查了50名笔试者的成绩如下表所示:
请你预测面试的分数线大约是多少?
(2)该市某学校从聘用的四男a、b、c、d和二女e、f中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
(1)随机调查了50名笔试者的成绩如下表所示:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 2 | 3 | 15 | 20 | 7 | 3 |
(2)该市某学校从聘用的四男a、b、c、d和二女e、f中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
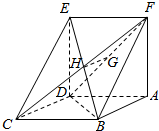 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点,记CD=x,V(x)表示四棱锥F-ABCD的体积.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点,记CD=x,V(x)表示四棱锥F-ABCD的体积.