题目内容
6.已知a>0,b>0,且a+b=ab,则a+$\frac{b}{4}$的最小值为( )| A. | 1 | B. | $\frac{7}{4}$ | C. | 2 | D. | $\frac{9}{4}$ |
分析 由a+b=ab得$\frac{1}{a}$+$\frac{1}{b}$=1,则a+$\frac{b}{4}$=(a+$\frac{b}{4}$)•($\frac{1}{a}$+$\frac{1}{b}$)=1+$\frac{1}{4}$+$\frac{a}{b}$+$\frac{b}{4a}$≥$\frac{5}{4}$+2•$\sqrt{\frac{a}{b}•\frac{b}{4a}}$=$\frac{5}{4}$+1=$\frac{9}{4}$.
解答 解:∵a+b=ab,∴$\frac{1}{a}$+$\frac{1}{b}$=1,则:
a+$\frac{b}{4}$=(a+$\frac{b}{4}$)•($\frac{1}{a}$+$\frac{1}{b}$)
=1+$\frac{1}{4}$+$\frac{a}{b}$+$\frac{b}{4a}$
≥$\frac{5}{4}$+2•$\sqrt{\frac{a}{b}•\frac{b}{4a}}$
=$\frac{5}{4}$+1=$\frac{9}{4}$,
即a+$\frac{b}{4}$的最小值为$\frac{9}{4}$,
当且仅当:a=$\frac{3}{2}$,b=3时,取得最小值,
故选:D.
点评 本题主要考查了基本不等式在求最值问题中的应用,体现了整体法的解题思想,属于基础题.

练习册系列答案
相关题目
16.在复平面内,复数$\frac{1}{1+i}$+i所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.执行如图所示的程序框图,则输出的S=( )
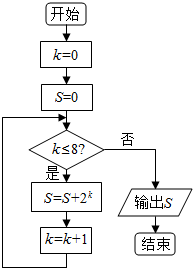

| A. | 1023 | B. | 512 | C. | 511 | D. | 255 |