题目内容
9.已知函数f(x)=alnx+x2.(Ⅰ)当a=1,函数g(x)=f(x)+$\frac{2}{x+1}$-x2,求g(x)在区间[1,+∞)上的最小值;
(Ⅱ)若存在x∈[1,e]时,使f(x)≤(a+2)x恒成立,求实数a的取值范围;
(Ⅲ)求证:ln(n+1)>$\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+…+\frac{1}{2n+1}$(n∈N+).
分析 (I)当a=1,x≥1,函数g(x)=lnx+$\frac{2}{x+1}$,g′(x)=$\frac{{x}^{2}+1}{x(x+1)^{2}}$>0,利用单调性即可得出.
(II)当x∈[1,e]时,x>lnx,不等式f(x)≤(a+2)x,化为$a≥\frac{{x}^{2}-2x}{x-lnx}$,令h(x)=$\frac{{x}^{2}-2x}{x-lnx}$,利用导数研究其单调性极值与最值即可得出.
(III)由(1)可得:x∈[1,+∞),lnx+$\frac{2}{x+1}$≥1,可得ln(x+1)>$\frac{x}{x+2}$,令x=$\frac{1}{n}$,则ln(n+1)-lnn>$\frac{1}{2n+1}$,利用“累加求和”即可得出.
解答 (I)解:当a=1,x≥1
函数g(x)=f(x)+$\frac{2}{x+1}$-x2=lnx+$\frac{2}{x+1}$,g′(x)=$\frac{1}{x}$-$\frac{2}{(x+1)^{2}}$=$\frac{{x}^{2}+1}{x(x+1)^{2}}$>0,
∴函数g(x)在区间[1,+∞)上单调递增,
因此当x=1时,函数g(x)取得极小值即最小值,g(1)=1.
(II)解:当x∈[1,e]时,x>lnx,不等式f(x)≤(a+2)x,化为$a≥\frac{{x}^{2}-2x}{x-lnx}$,
令h(x)=$\frac{{x}^{2}-2x}{x-lnx}$,则h′(x)=$\frac{(x-1)(x+2-2lnx)}{(x-lnx)^{2}}$,
令u(x)=x+2-2lnx,u′(x)=1-$\frac{2}{x}$=$\frac{x-2}{x}$,可知:当x=2时,函数u(x)取得最小值,u(2)=4-ln4>0,
可知:h′(x)≥0,因此函数h(x)在x∈[1,e]单调递增.
∴当x=1时,函数h(x)取得最小值,h(1)=-1,
∴a≥-1.
(III)证明:由(1)可得:x∈[1,+∞),lnx+$\frac{2}{x+1}$≥1,
∴ln(x+1)>$\frac{x}{x+2}$,
令x=$\frac{1}{n}$,则ln(n+1)-lnn>$\frac{1}{2n+1}$,
∴ln2-ln1>$\frac{1}{3}$,ln3-ln2>$\frac{1}{5}$,…,ln(n+1)-lnn>$\frac{1}{2n+1}$,
∴ln(n+1)>$\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+…+\frac{1}{2n+1}$(n∈N+).
点评 本题考查了利用导数研究其单调性极值与最值、恒成立问题等价转化方法、利用研究证明的结论证明不等式,考查了推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
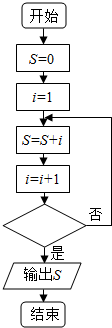
| A. | i>8 | B. | i>9 | C. | i>10 | D. | i>11 |
| A. | $\widehat{y}$=1.04x+2 | B. | $\widehat{y}$=1.04x+1.9 | C. | $\widehat{y}$=1.05x+1.9 | D. | $\widehat{y}$=1.9x+1.04 |