题目内容
规定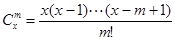 ,其中x∈R,m是正整数,且
,其中x∈R,m是正整数,且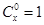 ,这是组合数
,这是组合数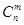 (n、m是正整数,且m≤n)的一种推广.
(n、m是正整数,且m≤n)的一种推广.
(1) 求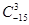 的值;
的值;
(2) 设x>0,当x为何值时,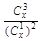 取得最小值?
取得最小值?
(3) 组合数的两个性质;
①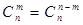 . ②
. ②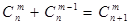 .
.
是否都能推广到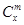 (x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(x∈R,m是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(1)-680(2)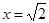
(3)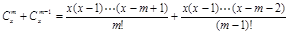
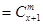
解析试题分析:解:(1)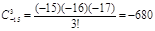 .
.
(2) 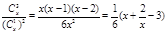 . ∵ x > 0 ,
. ∵ x > 0 , 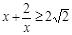 .
.
当且仅当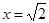 时,等号成立. ∴ 当
时,等号成立. ∴ 当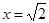 时,
时,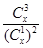 取得最小值.
取得最小值.
(3)性质①不能推广,例如当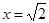 时,
时,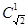 有定义,但
有定义,但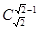 无意义;
无意义;
性质②能推广,它的推广形式是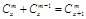 ,xÎR , m是正整数.
,xÎR , m是正整数.
事实上,当m=1时,有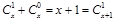 .
.
当m≥2时. 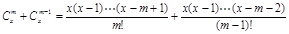
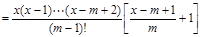
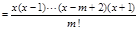
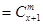 .
.
考点:组合数公式和性质
点评:主要是考查了组合数的公式的灵活的变换和求解运算能力,属于基础题。

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
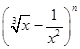 的展开式的二项式系数和为128.
的展开式的二项式系数和为128.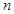 的值;
的值; 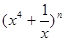 的展开式中,第三项的二项式系数比第二项的二项式系数大35。
的展开式中,第三项的二项式系数比第二项的二项式系数大35。  的值; (2)求展开式中的常数项。
的值; (2)求展开式中的常数项。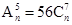 ,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.
,且(1-2x)n=a0+a1x+a2x2+a3x3+……+anxn.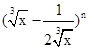 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列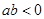 且
且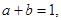 二项式
二项式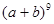 按
按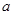 的降幂排列,展开后其第二项不大于第三项,求
的降幂排列,展开后其第二项不大于第三项,求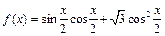
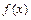 写成
写成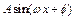 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;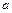 ,
,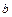 ,
,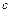 满足
满足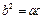 ,且边
,且边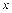 ,试求角
,试求角