题目内容
正四棱柱ABCD-A1B1C1D1中,AB=3,BB1=4.长为1的线段PQ在棱AA1上移动,长为3的线段MN在棱CC1上移动,点R在棱BB1上移动,则四棱锥R-PQMN的体积是
6
6
.分析:先根据题型的面积公式求出底面PQMN的面积,再求R到底面PQMN的距离,然后根据棱锥的体积公式求出四棱锥R-PQMN的体积即可.
解答: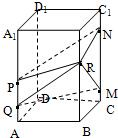 解:由题意可知底面PQMN的面积是
解:由题意可知底面PQMN的面积是
×3
=6
R到PQMN的距离即为点B到面AC1的距离为
四棱锥R-PQMN的体积是:
×6
×
=6
故答案为:6
 解:由题意可知底面PQMN的面积是
解:由题意可知底面PQMN的面积是 | 1+3 |
| 2 |
| 2 |
| 2 |
R到PQMN的距离即为点B到面AC1的距离为
3
| ||
| 2 |
四棱锥R-PQMN的体积是:
| 1 |
| 3 |
| 2 |
3
| ||
| 2 |
故答案为:6
点评:本题主要考查棱锥的体积,考查计算能力,抓住动中有静的思想,本题虽PQ与MN都在动但面PQMN的面积不变,是解题的关键,是基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
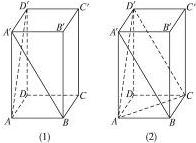 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是