题目内容
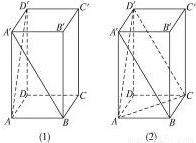
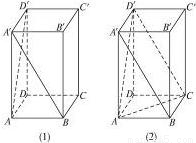
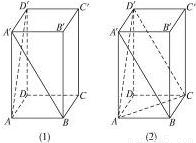
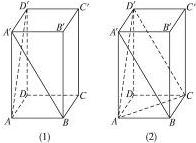如图（1），正四棱柱ABCD-A′B′C′D′中，AA′=2AB，则异面直线A′B与AD′所成的角的余弦值是分析：迁连接D′C、AC有，A′B∥D′C，再由异面直线所成角的定义?∠AD′C为异面直线A′B与AD′所成的角，放△AD′C中求解．
解答：解：如图（2），连接D′C、AC，则A′B∥D′C，
∴异面直线A′B与AD′所成的角等于∠AD′C、
令AB=a，∴AA′=2AB=2A、
∴AD′=D′C=
a，AC=
a．
△AD′C中，AD′=D′C=
a，AC=
a，
∴cos∠AD′C=
=
=
．
故答案为
．
∴异面直线A′B与AD′所成的角等于∠AD′C、
令AB=a，∴AA′=2AB=2A、
∴AD′=D′C=
| 5 |
| 2 |
△AD′C中，AD′=D′C=
| 5 |
| 2 |
∴cos∠AD′C=
| AD′2+D′C2-AC2 |
| 2AD′•D′C |
| 8a2 |
| 10a2 |
| 4 |
| 5 |
故答案为
| 4 |
| 5 |
点评：本题主要考查异面直线所成角的作法及求法，若在直角三形中可由三角函数定义求解，若在一般三角形中则用余弦定理求解．
练习册系列答案
相关题目
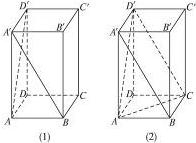如图（1），正四棱柱ABCD-A′B′C′D′中，AA′=2AB，则异面直线A′B与AD′所成的角的余弦值是________．
