题目内容
已知正四棱柱ABCD-A′B′C′D′的外接球直径为| 6 |
分析:以D为原点,以DA为x轴,以DC为y轴,以DD′为z轴,建立空间直角坐标系D-xyz,利用向量法能求出侧棱BB′与平面AB′C所成角的正弦值,再由三角函数的性质能求出结果.
解答:解:以D为原点,以DA为x轴,以DC为y轴,以DD′为z轴,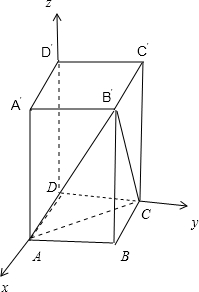
建立空间直角坐标系D-xyz,
∵正四棱柱ABCD-A′B′C′D′的外接球直径为
,底面边长AB=1,
∴DD′=
=2,
∴A(1,0,0),C(0,1,0),B′(1,1,2),B(1,1,0),
∴
=(0,0,-2),
=(0,1,2),
=(-1,1,0),
设平面ACB′的法向量
=(x,y,z),
∴
•
=0,
•
=0,
∴
,∴
=(2,2,-1),
设直线B′B与平面AB′C所成角为θ,
则sinθ=|cos<
,
>|=|
|=
,
∴cosθ=
=
,
∴tanθ=
.
故答案为:
.

建立空间直角坐标系D-xyz,
∵正四棱柱ABCD-A′B′C′D′的外接球直径为
| 6 |
∴DD′=
| 6-(1+1) |
∴A(1,0,0),C(0,1,0),B′(1,1,2),B(1,1,0),
∴
| B′B |
| AB′ |
| AC |
设平面ACB′的法向量
| n |
∴
| n |
| AB′ |
| n |
| AC |
∴
|
| n |
设直线B′B与平面AB′C所成角为θ,
则sinθ=|cos<
| B′B |
| n |
| 2 | ||
2×
|
| 1 |
| 3 |
∴cosθ=
1-
|
2
| ||
| 3 |
∴tanθ=
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查直线与平面所成角的正切值的求法,是中档题,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
 如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为
如图所示,已知正四棱柱ABCD-A1B1C1D1的底面边长为1,点E在棱AA1上,A1C∥平面EBD,截面EBD的面积为 如图,已知正四棱柱ABCD-A1B1C1D1与它的侧视图(或称左视图),E是DD1上一点,AE⊥B1C.
如图,已知正四棱柱ABCD-A1B1C1D1与它的侧视图(或称左视图),E是DD1上一点,AE⊥B1C. (2006•广州模拟)已知正四棱柱ABCD-A1B1C1D1,AB=BC=1,AA1=2,点E为CC1的中点,点F为BD1的中点.
(2006•广州模拟)已知正四棱柱ABCD-A1B1C1D1,AB=BC=1,AA1=2,点E为CC1的中点,点F为BD1的中点.