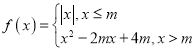题目内容
【题目】设函数![]() 由方程到
由方程到![]() 确定,对于函数
确定,对于函数![]() 给出下列命题:
给出下列命题:
①对任意![]()
![]() ,都有
,都有![]() 恒成立:
恒成立:
②![]()
![]() ,使得
,使得![]() 且
且![]() 同时成立;
同时成立;
③对于任意![]()
![]() 恒成立;
恒成立;
④对任意,![]()
![]()
![]() ,
,
都有![]() 恒成立.其中正确的命题共有( )
恒成立.其中正确的命题共有( )
A.1个B.2个C.3个D.4个
【答案】B
【解析】
分四类情况进行讨论,画出相对应的函数图象,由函数图象判断所给命题的真假性.
由方程![]() 知,
知,
当x≥0且y≥0时,方程为![]() y2=1;
y2=1;
当x<0且y<0时,方程为![]() y2=1,不成立;
y2=1,不成立;
当x≥0且y<0时,方程为![]() y2=1;
y2=1;
当x<0且y≥0时,方程为![]() y2=1;
y2=1;
作出函数f(x)的图象如图所示,
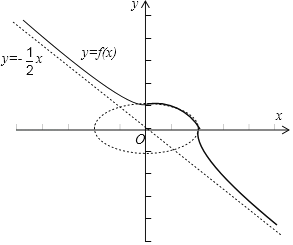
对于①,f(x)是定义域R上的单调减函数,则
对任意x1,x2∈R,x1≠x2,都有![]() 恒成立,①正确;
恒成立,①正确;
对于②,假设点(a,b)在第一象限,则点(b,a)也在第一象限,
所以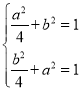 ,该方程组没有实数解,所以该情况不可能;
,该方程组没有实数解,所以该情况不可能;
假设点(a,b)在第四象限,则点(b,a)在第二象限,
所以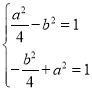 ,该方程组没有实数解,所以该种情况不可能;
,该方程组没有实数解,所以该种情况不可能;
同理点(a,b)在第二象限,则点(b,a)在第四象限,也不可能.
故该命题是假命题.
对于③,由图形知,对于任意x∈R,有f(x)![]() x,
x,
即2f(x)+x>0恒成立,③正确;
对于④,不妨令t![]() ,则tf(x1)+(1﹣t)f(x2)﹣f[tx1+(1﹣t)x2]>0为
,则tf(x1)+(1﹣t)f(x2)﹣f[tx1+(1﹣t)x2]>0为
![]() f(
f(![]() ),不是恒成立,所以④错误.
),不是恒成立,所以④错误.
综上知,正确的命题序号是①③.
故选:B.

练习册系列答案
相关题目