Question

11．如图，四边形ABED是边长为2的菱形，△CDE为正三角形，B，E，C三点共线，现将△ABD沿BD折起形成三棱锥A′-BCD．
（1）求证：A′E⊥BD；
（2）若平面A′BD⊥平面ABCD，求直线CD与平面A′BC所成角的正弦值．

Answer 1

分析 （1）利用菱形的几何性质得出A′O⊥BD，OE⊥BD，转化为证明A′E⊥面A¹OE，
即可利用线面的垂直，直线的垂直求证．
（2）建立空间坐标系得出$\overrightarrow{DC}$=（2，0，0），$\overrightarrow{{A}^{′}B}$=（0，-$\sqrt{3}$，-$\sqrt{3}$），$\overrightarrow{{A}^{′}C}$=（2，$\sqrt{3}$，-$\sqrt{3}$），求解法向量得出$\overrightarrow{n}$=（-3，$\sqrt{3}$，$-\sqrt{3}$），
再利用向量的数量积得出空间即可．

解答 解：（1）取BD中点O，连接A′O，OE，
∵四边形ABED是边长为2的菱形，
∴A′O⊥BD，OE⊥BD，
∵A′O∩OE=O，
∴A′E⊥面A¹OE，
∵A′E?面A¹OE，
∴A′E⊥BD；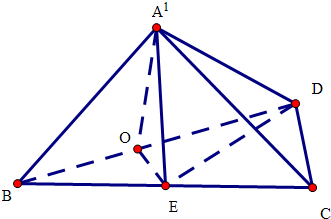
（2）（2）以OE，OD，OA′为x，y，z轴，
∵四边形ABED是边长为2的菱形，△CDE为正三角形，B，E，C三点共线，
∴D（0，$\sqrt{3}$，0），B（0，-$\sqrt{3}$，0），C（2，$\sqrt{3}$，0），A′（0，0，$\sqrt{3}$），
即$\overrightarrow{DC}$=（2，0，0），$\overrightarrow{{A}^{′}B}$=（0，-$\sqrt{3}$，-$\sqrt{3}$），$\overrightarrow{{A}^{′}C}$=（2，$\sqrt{3}$，-$\sqrt{3}$），
∵设$\overrightarrow{n}$=（x，y，z）为平面A′BC的法向量，
∴$\overrightarrow{{A}^{′}B}$•$\overrightarrow{n}$=0，$\overrightarrow{n}$$•\overrightarrow{{A}^{′}C}$=0，
所以得出$\left\{\begin{array}{l}{y+z=0}\\{2x+\sqrt{3}y-\sqrt{3}z=0}\end{array}\right.$
取x=-3，y=$\sqrt{3}$，z=$-\sqrt{3}$
$\overrightarrow{n}$=（-3，$\sqrt{3}$，$-\sqrt{3}$），
∵$\overrightarrow{n}$$•\overrightarrow{DC}$=-6，|$\overrightarrow{DC}$|=2，|$\overrightarrow{n}$|=$\sqrt{15}$，
∴cos＜$\overrightarrow{n}$，$\overrightarrow{DC}$＞=$-\frac{\sqrt{15}}{5}$，
∴直线CD与平面A′BC所成角的正弦值sinθ=$\frac{\sqrt{15}}{5}$，

点评 本题考查了空间直线平面所成的角，空间直线的位置关系 判断垂直问题，化为立体为平面解决，利用空间坐标系求解空间较大问题．