题目内容
设 是椭圆
是椭圆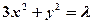 上的两点,点
上的两点,点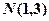 是线段
是线段 的中点,
的中点,
线段 的垂直平分线与椭圆相交于
的垂直平分线与椭圆相交于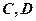 两点.
两点.
(1)确定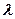 的取值范围,并求直线
的取值范围,并求直线 的方程;
的方程;
(2)试判断是否存在这样的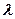 ,使得
,使得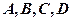 四点在同一个圆上?并说明理由.
四点在同一个圆上?并说明理由.
 是椭圆
是椭圆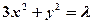 上的两点,点
上的两点,点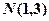 是线段
是线段 的中点,
的中点,线段
 的垂直平分线与椭圆相交于
的垂直平分线与椭圆相交于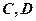 两点.
两点.(1)确定
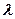 的取值范围,并求直线
的取值范围,并求直线 的方程;
的方程;(2)试判断是否存在这样的
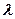 ,使得
,使得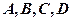 四点在同一个圆上?并说明理由.
四点在同一个圆上?并说明理由.(1)解法一:设直线 的方程为
的方程为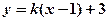 ,代入
,代入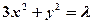
整理得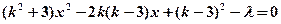 ①
①
设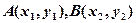 ,
,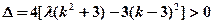 ,② 且
,② 且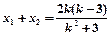
由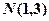 是线段
是线段 的中点,得
的中点,得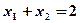 ,解得
,解得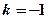 ,代入②得
,代入②得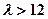
所以直线 的方程为
的方程为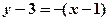 ,即
,即 (5分)
(5分)
解法二:设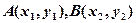 ,(点差)则有
,(点差)则有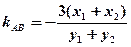 ,
,
∵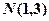 是线段
是线段 的中点,
的中点,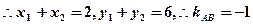
又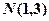 在椭圆内部,
在椭圆内部,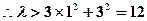 ,即
,即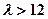 ,
,
∴直线 的方程为
的方程为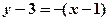 ,即
,即
(2)解法一:因为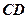 垂直平分
垂直平分 ,所以直线
,所以直线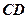 的方程为
的方程为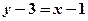 ,
,
即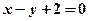 ,代入椭圆方程,整理得
,代入椭圆方程,整理得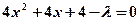
设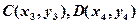 ,
,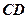 的中点
的中点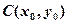 ,
,
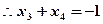 且
且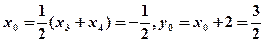 ,
,
即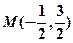 ,由弦长公式得
,由弦长公式得 ③,
③,
将直线 的方程
的方程 代入椭圆方程得
代入椭圆方程得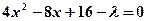 ④,
④,
同理可得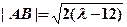 ⑤ (9分)
⑤ (9分)
因为当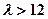 时,
时,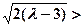
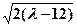 ,所以
,所以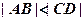
假设存在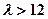 ,使
,使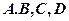 四点共圆,则
四点共圆,则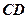 必为圆的直径,点
必为圆的直径,点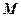 为圆心。
为圆心。
点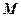 到直线
到直线 的距离
的距离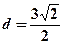 ⑥,
⑥,
于是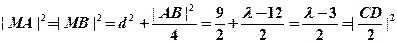 ,
,
故当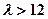 时,
时,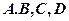 在以
在以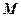 为圆心,
为圆心,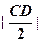 为半径的圆上 (12分)
为半径的圆上 (12分)
 的方程为
的方程为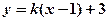 ,代入
,代入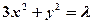
整理得
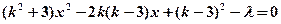 ①
①设
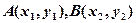 ,
,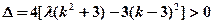 ,② 且
,② 且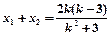
由
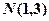 是线段
是线段 的中点,得
的中点,得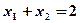 ,解得
,解得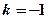 ,代入②得
,代入②得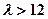
所以直线
 的方程为
的方程为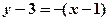 ,即
,即 (5分)
(5分)解法二:设
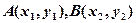 ,(点差)则有
,(点差)则有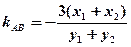 ,
,∵
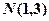 是线段
是线段 的中点,
的中点,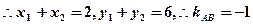
又
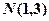 在椭圆内部,
在椭圆内部,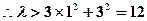 ,即
,即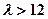 ,
,∴直线
 的方程为
的方程为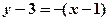 ,即
,即
(2)解法一:因为
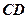 垂直平分
垂直平分 ,所以直线
,所以直线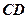 的方程为
的方程为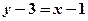 ,
,即
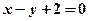 ,代入椭圆方程,整理得
,代入椭圆方程,整理得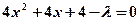
设
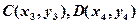 ,
,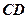 的中点
的中点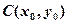 ,
,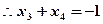 且
且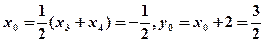 ,
,即
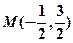 ,由弦长公式得
,由弦长公式得 ③,
③,将直线
 的方程
的方程 代入椭圆方程得
代入椭圆方程得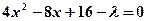 ④,
④,同理可得
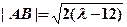 ⑤ (9分)
⑤ (9分)因为当
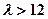 时,
时,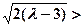
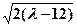 ,所以
,所以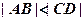
假设存在
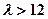 ,使
,使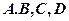 四点共圆,则
四点共圆,则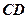 必为圆的直径,点
必为圆的直径,点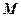 为圆心。
为圆心。点
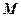 到直线
到直线 的距离
的距离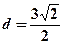 ⑥,
⑥,于是
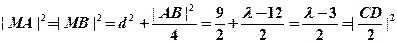 ,
,故当
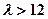 时,
时,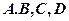 在以
在以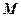 为圆心,
为圆心,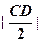 为半径的圆上 (12分)
为半径的圆上 (12分)答案

练习册系列答案
相关题目
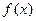 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“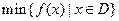 ”表示函数
”表示函数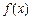 在集合D上的最小值,“
在集合D上的最小值,“ ”表示函数
”表示函数 ,
,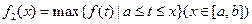 ,
,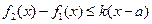 对任意的
对任意的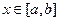 成立,则称函数
成立,则称函数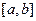 上的“第k类压缩函数”.
上的“第k类压缩函数”.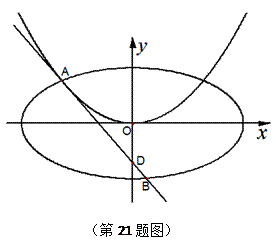
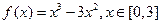 ,求
,求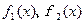 的解析式;
的解析式;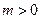 ,函数
,函数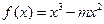 是
是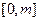 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围. 是椭圆
是椭圆 上的两点,点
上的两点,点 是线段
是线段 的中点,线段
的中点,线段 两点.
两点. 的取值范围,并求直线
的取值范围,并求直线 四点在同一个圆上?并说明理由.
四点在同一个圆上?并说明理由.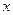 轴上的椭圆
轴上的椭圆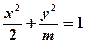 的离心率为
的离心率为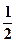 ,则m=( )
,则m=( )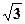
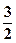
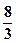
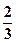
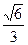

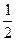
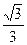
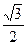
 (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为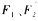 ,短轴两个端点为.A、B且四边形
,短轴两个端点为.A、B且四边形 是边长为2的正方形.
是边长为2的正方形.
 圆的方程;
圆的方程; 为定值;
为定值; 过直线DP,MQ的交点.若存在,求出点Q的坐标;若不存在,说明理由.
过直线DP,MQ的交点.若存在,求出点Q的坐标;若不存在,说明理由.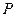 在椭圆
在椭圆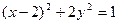 上,则
上,则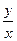 的最大值是( )
的最大值是( )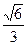
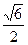
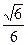
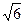

 的两个焦点为
的两个焦点为 、
、 ,且
,且 ,弦AB过点
,弦AB过点 的周长为__________
的周长为__________ 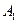 的正上方有一个光源
的正上方有一个光源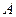 ,
,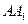 与球相切,
与球相切,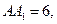 球在桌面上的投影是一个椭圆,则这个椭圆的离心率等于( )
球在桌面上的投影是一个椭圆,则这个椭圆的离心率等于( )