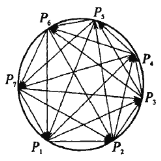
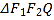题目内容
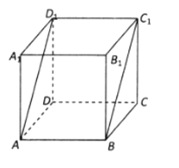
【题目】已知圆周上有七个不同的点,以其中任意一点为始点,另一点为终点作向量,作出所有的向量(对于点![]() 、
、![]() ,若作出向量
,若作出向量![]() ,则不再作向量
,则不再作向量![]() ).若其中某四点所确定的凸四边形的四条边是首尾相接的四个向量,则称其为“零四边形”.试求以这七个点中四个点为顶点的凸四边形中,零四边形个数的最大值
).若其中某四点所确定的凸四边形的四条边是首尾相接的四个向量,则称其为“零四边形”.试求以这七个点中四个点为顶点的凸四边形中,零四边形个数的最大值
【答案】28
【解析】
设圆周上这七个点分别为![]() ,
,![]() ,…,
,…,![]() .以点
.以点![]() 为始点的向量个数为
为始点的向量个数为![]() ,则
,则![]() ,且
,且![]() .
.
先求在![]() 个凸四边形中“非零四边形”个数的最小值.
个凸四边形中“非零四边形”个数的最小值.
易知非零四边形只有如下两类情形:
第一类:有且只有一个顶点是两边向量的始点的非零四边形(如图).

第二类:恰有两个顶点是两边向量的始边的非零四边形(如图).
(1)当整个图形中含有第二类非零四边形时,易知在第二类非零四边形的四个顶点的基础上,每增加一个点,则此五点形就比原四点形增加四个凸四边形,且作图易知这四个凸四边形均是非零四边形.
于是,在整个七点图形中的35个凸四边形中,若有一个是第二类非零四边形,则在此非零四边形的基础上增加三点,至少要增加![]() 12个非零四边形.由此知,此时图中至少有13个非零四边形.
12个非零四边形.由此知,此时图中至少有13个非零四边形.
(2)当七点图中不含第二类非零四边形,即其中只含有第一类非零四边形和零四边形,则问题可转化为只要求出其中第一类非零四边形个数的最小值即可.
而第一类非零四边形的四个顶点中有且只有一个顶点是此非零四边形的四个边向量的两个向量的始点,且这两个向量夹有一个对角线向量.当这三个向量确定时,则确定一个非零四边形.从而,当图中不含第二类非零四边形时,图中含第一类非零四边形的个数
![]() .
.
因为![]() ,所以,
,所以,![]() 有最小值.
有最小值.
若![]() ,
,![]() ,…,
,…,![]() 中有某个
中有某个![]() 的值小于3,则其中必有
的值小于3,则其中必有![]() 的值大于或等于4.
的值大于或等于4.
而![]() ,
,![]() ,
,![]() ,又
,又![]() ,则必有
,则必有![]() .
.
若![]() ,
,![]() ,…,
,…,![]() 均不小于3,由
均不小于3,由![]() 知,只有
知,只有![]() ,
,![]() .
.
下面通过作图说明![]() 的图形是存在的(如图)
的图形是存在的(如图)
图中共有七个非零四边形.
①![]() ,②
,②![]() ,
,
③![]() ;④
;④![]() ,
,
⑤![]() ,⑥
,⑥![]() ,
,
⑦![]() .
.
故![]() 的最小值为
的最小值为![]() .
.
因此,所求的零四边形个数的最大值为![]() .
.

【题目】为了调查某地区70岁以上老人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了100位70岁以上老人,结果如下:
男 | 女 | |
需要 | 18 | 5 |
不需要 | 32 | 45 |
(1)估计该地区70岁以上老人中,男、女需要志愿者提供帮助的比例各是多少?
(2)能否有![]() 的把握认为该地区70岁以上的老人是否需要志愿者提供帮助与性别有关;
的把握认为该地区70岁以上的老人是否需要志愿者提供帮助与性别有关;
(3)根据(2)的结论,能否提供更好的调查方法来估计该地区70岁以上老人中,需要志愿者提供帮助的老人的比例?说明理由.
附:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,
,![]() .
.
【题目】画糖人是一种以糖为材料在石板上进行造型的民间艺术.某糖人师傅在公园内画糖人,每天卖出某种糖人的个数与价格相关,其相关数据统计如下表:
每个糖人的价格 | 9 | 10 | 11 | 12 | 13 |
卖出糖人的个数 | 54 | 50 | 46 | 43 | 39 |
(1)根据表中数据求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若该种造型的糖人的成本为2元/个,为使糖人师傅每天获得最大利润,则该种糖人应定价多少元?(精确到1元)
参考公式:回归直线方程![]() ,其中
,其中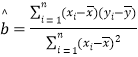 ,
,![]() .
.
【题目】随着电子商务的发展,人们的购物习惯正在改变,基本上所有的需求都可以通过网络购物解决.小王是位网购达人,每次购买商品成功后都会对电商的商品和服务进行评价.现对其近年的200次成功交易进行评价统计,统计结果如下表所示.
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 80 | 40 | 120 |
对商品不满意 | 70 | 10 | 80 |
合计 | 150 | 50 | 200 |
(1)是否有![]() 的把握认为商品好评与服务好评有关? 请说明理由;
的把握认为商品好评与服务好评有关? 请说明理由;
(2)现从这200次交易中,按照“对商品好评”和“对商品不满意”采用分层抽样取出5次交易,然后从这5次交易中任选两次进行观察,求这两次交易中恰有一次“对商品好评”的概率.
附: (其中
(其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|