题目内容
【题目】当
时，不等式
成立，则实数k的取值范围是______________.
【答案】k∈（﹣∞，1]
【解析】
此题先把常数k分离出来，再构造成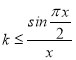
再利用导数求函数的最小值，使其最小值大于等于k即可．
由题意知：
∵当0≤x≤1时 
（1）当x＝0时，不等式恒成立 k∈R
（2）当0＜x≤1时，不等式可化为
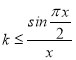
要使不等式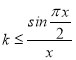恒成立，则k
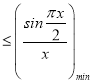成立
令f（x）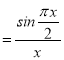
x∈（0，1]
即 f '（x）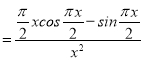
再令g（x）
g'（x）
∵当0＜x≤1时，g'（x）＜0
∴g（x）为单调递减函数
∴g（x）＜g（0）＝0
∴f '（x）＜0
即函数f（x）为单调递减函数
所以 f（x）min＝f（1）＝1 即k≤1
综上所述，由（1）（2）得 k≤1
故答案为： k∈（﹣∞，1]．
【题目】为了研究某种细菌的繁殖个数y随天数x的变化情况，收集数据如下：
天数x | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数y | 6 | 12 | 25 | 49 | 95 | 190 |
（1）根据散点图，判断
与
哪一个适合作为y关于x的回归方程类型；（给出判断即可，不用说明理由）
（2）根据（1）中的判断及表中数据，求y关于x的回归方程
参考数据：
，
，
，
，
，
参考公式：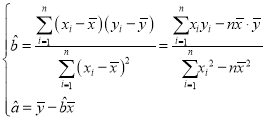
【题目】新冠状病毒严重威胁着人们的身体健康，我国某医疗机构为了调查新冠状病毒对我国公民的感染程度，选了某小区的
位居民调查结果统计如下：
感染 | 不感染 | 合计 | |
年龄不大于 |
| ||
年龄大于 |
| ||
合计 |
|
|
（1）根据已知数据，把表格数据填写完整；
（2）能否在犯错误的概率不超过
的前提下认为感染新冠状病与不同年龄有关？
（3）已知在被调查的年龄大于
岁的感染者中有
名女性，其中
位是女教师，现从这名女性中随机抽取
人，求至多有
位教师的概率．
附：
，
.
|
|
|
|
|
|
|
|
|
|
【题目】为了研究“教学方式”对教学质量的影响，某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学（勤奋程度和自觉性都一样）.以下茎叶图为甲、乙两班（每班均为20人）学生的数学期末考试成绩．
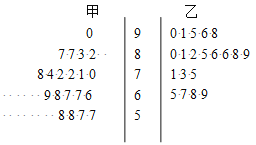
（1）学校规定：成绩不低于75分的为优秀．请画出下面的
列联表．
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
（2）判断有多大把握认为“成绩优秀与教学方式有关”．
下面临界值表仅供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式： 
