题目内容
已知数列 的前
的前 项和
项和 。
。
(1)求数列的通项公式;
(2)求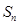 的最大或最小值。
的最大或最小值。
(1)an=2n-49(n N*);(2)当n=24时,Sn有最大值576
解析试题分析:(1)利用递推公式an=Sn-Sn-1可求
(2)若使Sn最小,则有an<0,an+1≥0,求出n的值,代入可求
(1)当n=1时,a1=S1
当n>1时,an=Sn-Sn -1=2n-49 ∴an=2n-49(n N*)
(2)Sn=(n-24)2+576
当n=24时,Sn有最大值576
考点:本试题主要考查了利用数列的递推公式an=Sn-Sn-1求解数列的通项公式,还主要考查了求解数列和的最小值问题,主要利用数列的单调性,则满足an<0,an+1≥0.
点评:解决该试题的关键是前n项和的最大值取得要满足数列的单调性,则满足an<0,an+1≥0.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
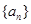 的各项均为正数,
的各项均为正数,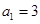 ,前
,前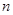 项和为
项和为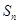 ,
,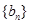 为等比数列,
为等比数列, 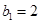 ,且
,且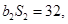
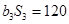 .
.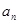 与
与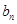 ;
;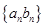 的前
的前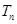 。
。 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 。
。 求证:数列
求证:数列 若
若 ,
, 为数列
为数列 的前
的前 满足:
满足: ,
, ,
, .
. 及前n项和
及前n项和 =
= (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和 .
.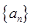 的前n项和
的前n项和 (n为正整数)。
(n为正整数)。 ,求证数列
,求证数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,求
,求 .
. 满足
满足 (
( ,
, .
. ,且
,且 ,求证:
,求证:  .
. 的前
的前 项和记为
项和记为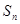 ,已知
,已知 .
. ;(2)若
;(2)若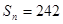 ,求
,求 ,求数列
,求数列 的前
的前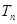 .
.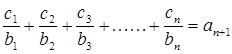 ,
, 中,
中,  求
求 的值。
的值。