题目内容
(本小题12分)等差数列 的前
的前 项和记为
项和记为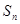 ,已知
,已知 .
.
(1)求数列 的通项
的通项 ;(2)若
;(2)若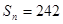 ,求
,求 ;(3)令
;(3)令 ,求数列
,求数列 的前
的前 项和
项和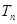 .
.
(1)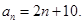 ;(2)
;(2)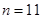 ;(3)
;(3)

解析试题分析:(1)由 可建立关于a1和d的方程,解出a1和d的值,得到数列
可建立关于a1和d的方程,解出a1和d的值,得到数列 的通项
的通项 .(2)根据
.(2)根据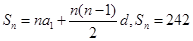 可建立关于n的方程解出n的值.
可建立关于n的方程解出n的值.
(3)因为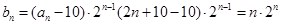 ,显然应采用错位相减的方法求和.
,显然应采用错位相减的方法求和.
(1)由 ,得方程组
,得方程组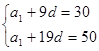 ,
,
解得
 .....................3分
.....................3分
(2)由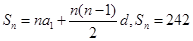 得方程
得方程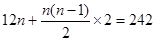
解得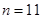 或
或 (舍去),
(舍去),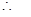
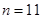 .....................6分
.....................6分
(3)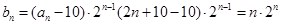 .....................7分
.....................7分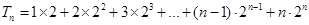
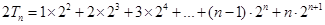 .....................9分
.....................9分
两式相减得: .....................10分
.....................10分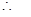

=-
 =
= .....................12分
.....................12分
考点:等差数列的通项公式及前n项和公式,以及错位相减法求和.
点评:错位相减法求和主要适应用一个等差数列与一个等比数列对应项的积构成的数列,其前n项和可考虑错位相减法.

练习册系列答案
相关题目
(本小题满分14分)
已知函数 的图像经过点
的图像经过点 .
.
(1)求该函数的解析式;
(2)数列 中,若
中,若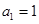 ,
, 为数列
为数列 的前
的前 项和,且满足
项和,且满足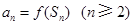 ,
,
证明数列 成等差数列,并求数列
成等差数列,并求数列 的通项公式;
的通项公式;
(3)另有一新数列 ,若将数列
,若将数列 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
 |
  |
   |
    |
 构成的数列即为数列
构成的数列即为数列 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当 时,求上表中第
时,求上表中第 行所有项的和.
行所有项的和. 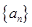 的前
的前 项和记为
项和记为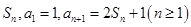
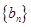 的各项为正,其前
的各项为正,其前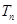 ,且
,且 ,又
,又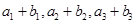 成等比数列,求
成等比数列,求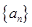 是首项为
是首项为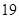 ,公差为
,公差为 的等差数列.
的等差数列.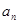 ;
; 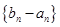 是首项为
是首项为 ,公比为
,公比为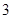 的等比数列,求数列
的等比数列,求数列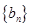 的通项公式及其前
的通项公式及其前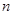 项和
项和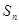 .
. 的前
的前 项和
项和 。
。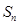 的最大或最小值。
的最大或最小值。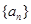 的前
的前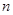 项和为
项和为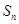 ,
,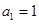 ,且
,且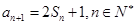 .
.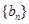 的各项均为正数,其前
的各项均为正数,其前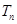 ,且
,且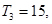 又
又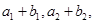
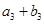 成等比数列,求
成等比数列,求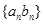 的前
的前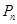 .
.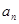 }的前n项和为
}的前n项和为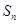 , 满足
, 满足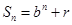 (
(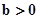
 均为常数)
均为常数)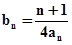
 ,求数列
,求数列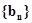 的前
的前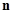 项的和
项的和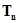 .(6分)
.(6分) 的首项
的首项 的等比数列,其前
的等比数列,其前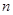 项和
项和 中
中 ,
, ,
, ,求证:
,求证:
 ,
, ,
, ,
, ,求数列
,求数列 的前
的前 项和
项和 。
。