题目内容
如图,直三棱柱 的侧棱长为3,
的侧棱长为3, ,且
,且 ,
,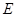 、
、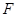 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且
(1)证明:无论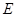 在何处,总有
在何处,总有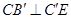 ;
;
(2)当三棱柱 .的体积取得最大值时,求异面直线
.的体积取得最大值时,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.

 的侧棱长为3,
的侧棱长为3, ,且
,且 ,
,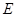 、
、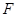 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且
(1)证明:无论
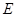 在何处,总有
在何处,总有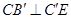 ;
;(2)当三棱柱
 .的体积取得最大值时,求异面直线
.的体积取得最大值时,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
(1)详见解析;(2)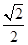 .
.
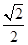 .
.试题分析:(1)利用正方形的性质,线面垂直的判定与性质定理求解;(2)利用三棱柱的体积公式,均值不等式求得.
试题解析:
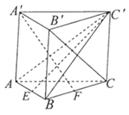
(1)∵
 是正方形,∴
是正方形,∴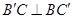 ,
,又
 ,
,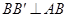 ,
,∴
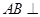 平面
平面 , (4分)
, (4分)∴
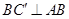 ,
,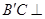 平面
平面 ,
,又
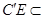 平面
平面 ,∴
,∴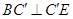 . (6分)
. (6分)(2)设三棱锥
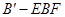 的体积为
的体积为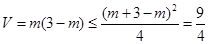 ,
,当
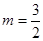 时取等号, (8分)
时取等号, (8分)故当
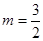 时,即
时,即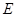 、
、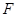 分别是棱
分别是棱 、
、 上的中点时,体积最大,
上的中点时,体积最大,则
 为所求.
为所求.∴
 ,
,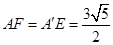 ,
, ,∴
,∴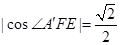 . (12分)
. (12分)
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 .
.
 中,直线
中,直线 和平面
和平面 所成角的余弦值大小为( )
所成角的余弦值大小为( )



 中,
中, 与
与 、
、 所成角均为
所成角均为 ,
, ,且
,且 ,则
,则 与
与 所成角的余弦值为( )
所成角的余弦值为( )
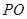 中,已知
中,已知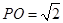 ,⊙O的直径
,⊙O的直径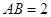 ,
,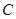 是
是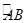 的中点,
的中点,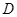 为
为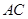 的中点.
的中点.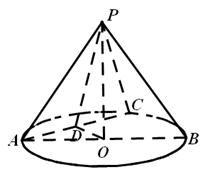
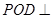 平面
平面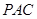 ;
;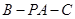 的余弦值.
的余弦值.  是直三棱柱,
是直三棱柱, 为直角,点
为直角,点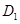 、
、 分别是
分别是 、
、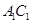 的中点,若
的中点,若 ,则
,则 与
与 所成角的余弦值是( )
所成角的余弦值是( )





 中,若
中,若 ,则
,则 与
与 所成角为( )
所成角为( )


