题目内容
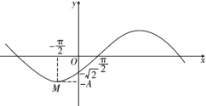
【题目】已知椭圆![]()
(1)求椭圆![]() 的标准方程和离心率;
的标准方程和离心率;
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,且满足
两点,且满足![]() .若存在,求出直线
.若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)存在,7x﹣
;(2)存在,7x﹣![]() +3
+3![]() =0或7x+
=0或7x+![]() ﹣3
﹣3![]() =0
=0
【解析】
(1)将椭圆方程化为标准方程,可得a,b,c,由离心率公式可得所求值;
(2)假设存在过点P(0,3)的直线l与椭圆C相交于A,B两点,且满足![]() ,可设直线l的方程为x=m(y﹣3),联立椭圆方程,消去x可得y的二次方程,运用韦达定理和判别式大于0,再由向量共线的坐标表示,化简整理解方程,即可判断是否存在这样的直线.
,可设直线l的方程为x=m(y﹣3),联立椭圆方程,消去x可得y的二次方程,运用韦达定理和判别式大于0,再由向量共线的坐标表示,化简整理解方程,即可判断是否存在这样的直线.
(1)由![]() ,得
,得![]() ,进而
,进而![]() ,
,![]() ;
;
(2)假设存在过点P(0,3)的直线l与椭圆C相交于A,B两点,且满足![]() ,
,
可设直线l的方程为x=m(y﹣3),联立椭圆方程x2+2y2=4,
可得(2+m2)y2﹣6m2y+9m2﹣4=0,△=36m4﹣4(2+m2)(9m2﹣4)>0,即m2<![]() ,
,
设A(x1,y1),B(x2,y2),可得y1+y2=![]() ,y1y2=
,y1y2=![]() ,①
,①
由![]() ,可得(x2,y2﹣3)=2(x1,y1﹣3),即y2﹣3=2(y1﹣3),即y2=2y1﹣3,②
,可得(x2,y2﹣3)=2(x1,y1﹣3),即y2﹣3=2(y1﹣3),即y2=2y1﹣3,②
将②代入①可得3y1﹣3=![]() ,y1(2y1﹣3)=
,y1(2y1﹣3)=![]() ,
,
消去y1,可得![]()
![]() =
=![]() ,解得m2=
,解得m2=![]()
![]() ,所以
,所以![]() ,
,
故存在这样的直线l,且方程为7x﹣![]() y+3
y+3![]() =0或7x+
=0或7x+![]() y﹣3
y﹣3![]() =0.
=0.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(1)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(2)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,下个月分别在两个不同的网店进行销售,求这两个网店下个月获得奖励的总额![]() 的分布列及其数学期望.
的分布列及其数学期望.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为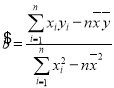 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
【题目】企业需为员工缴纳社会保险,缴费标准是根据职工本人上一年度月平均工资(单位:元)的![]() 缴纳,
缴纳,
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y(单位:元)与年份序号t的统计如下表:
(1)求出t关于t的线性回归方程![]() ;
;
(2)试预测2019年该员工的月平均工资为多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(注: ,
,![]() ,其中
,其中![]() )
)