题目内容
【题目】从![]() ,
,![]() ,
,![]() 等8人中选出5人排成一排.
等8人中选出5人排成一排.
(1)![]() 必须在内,有多少种排法?
必须在内,有多少种排法?
(2)![]() ,
,![]() ,
,![]() 三人不全在内,有多少种排法?
三人不全在内,有多少种排法?
(3)![]() ,
,![]() ,
,![]() 都在内,且
都在内,且![]() ,
,![]() 必须相邻,
必须相邻,![]() 与
与![]() ,
,![]() 都不相邻,都多少种排法?
都不相邻,都多少种排法?
(4)![]() 不允许站排头和排尾,
不允许站排头和排尾,![]() 不允许站在中间(第三位),有多少种排法?
不允许站在中间(第三位),有多少种排法?
【答案】(1)4200种;(2)5520;(3)240;(4)4440
【解析】
(1)只需从余下的7人中选4人出来排列即可;
(2)采用间接法;
(3)先从余下5人中选2人有![]() 种不同结果,由于
种不同结果,由于![]() ,
,![]() 必须相邻,
必须相邻,![]() 与
与![]() ,
,![]() 都不相邻,利用捆绑法、插空法即可解决;
都不相邻,利用捆绑法、插空法即可解决;
(4)分所选的5人无A、B,有A、无B,无A、有B,有A、B四种情况讨论即可.
(1)由题意,先从余下的7人中选4人共有![]() 种不同结果,再将这4人与A进行全排
种不同结果,再将这4人与A进行全排
列有![]() 种不同的排法,故由乘法原理可知共有
种不同的排法,故由乘法原理可知共有![]() 种不同排法;
种不同排法;
(2)从8人中任选5人排列共有![]() 种不同排法,
种不同排法,![]() ,
,![]() ,
,![]() 三人全在内有
三人全在内有![]() 种不同排
种不同排
法,由间接法可得![]() ,
,![]() ,
,![]() 三人不全在内共有
三人不全在内共有![]()
![]() 种不同排法;
种不同排法;
(3)因![]() ,
,![]() ,
,![]() 都在内,所以只需从余下5人中选2人有
都在内,所以只需从余下5人中选2人有![]() 种不同结果,
种不同结果,![]() ,
,![]() 必须
必须
相邻,有![]() 种不同排法,由于
种不同排法,由于![]() 与
与![]() ,
,![]() 都不相邻,先将选出的2人进行全排列共有
都不相邻,先将选出的2人进行全排列共有![]()
种不同排法,再将A、B这个整体与C插入到选出的2人所产生的3各空位中有![]() 种不同
种不同
排法,由乘法原理可得共有![]() 种不同排法;
种不同排法;
(4)分四类:
第一类:所选的5人无A、B,共有![]() 种排法;
种排法;
第二类:所选的5人有A、无B,共有![]() 种排法;
种排法;
第三类:所选的5人无A、有B,共有![]() 种排法;
种排法;
第四类:所选的5人有A、B,若A排中间时,有![]() 种排法,
种排法,
若A不排中间时,有![]() 种排法,共有
种排法,共有![]() 种排法;
种排法;
综上,共有4440种不同排法.

 名校课堂系列答案
名校课堂系列答案【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(Ⅱ)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销量量不低于10万件的概率.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为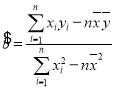 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
【题目】某工厂生产![]() ,
,![]() ,
,![]() 三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
普通型 | 精品型 | |
纪念品 | 800 | 200 |
纪念品 |
| 150 |
纪念品 | 500 | 350 |
现采用分层抽样的方法在这一天生产的纪念品中抽取100个,其中有![]() 种纪念品40个.
种纪念品40个.
(1)若再用分层抽样的方法在所有![]() 种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
(2)从![]() 种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,
种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,![]() ,
,![]() ,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求
,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求![]() 的值.
的值.