题目内容
【题目】若数列![]() 满足条件:存在正整数
满足条件:存在正整数![]() ,使得
,使得![]() 对一切
对一切![]() ,
,![]() 都成立,则称数列
都成立,则称数列![]() 为
为![]() 级等比数列;
级等比数列;
(1)已知数列![]() 为2级等比数列,且前四项分别为
为2级等比数列,且前四项分别为![]() 、
、![]() 、
、![]() 、
、![]() ,求
,求![]() 的值;
的值;
(2)若![]() (
(![]() 为常数),且数列
为常数),且数列![]() 是3级等比数列,求
是3级等比数列,求![]() 所有可能的值,并求
所有可能的值,并求![]() 取最小正值时数列
取最小正值时数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)证明:正数数列![]() 为等比数列的充要条件是数列
为等比数列的充要条件是数列![]() 既为2级等比数列,也为3级等比数列;
既为2级等比数列,也为3级等比数列;
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)证明详见解析.
;(3)证明详见解析.
【解析】
(1)利用定义,求出![]() 、
、![]() ,即可求
,即可求![]() 的值;
的值;
(2)根据![]() 是3级等比数列,列出方程,即可求
是3级等比数列,列出方程,即可求![]() 所有可能值的集合,从而求
所有可能值的集合,从而求![]() 取最小正值时数列
取最小正值时数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)根据数列![]() 为
为![]() 级等比数列的定义,分充分性与必要性进行证明即可.
级等比数列的定义,分充分性与必要性进行证明即可.
(1)解:由题意,![]()
![]() ,
,
![]() ,
,
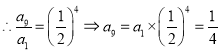 ,
,
![]() .
.
(2)解:![]() 是3级等比数列,
是3级等比数列,
![]() ,
,
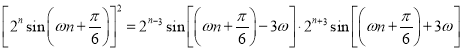
![]()
![]() ,
,
![]() ,
,
整理为:![]() ,
,
即![]() ,
,![]() ,
,![]()
![]() ,
,
![]() 的最小正值是
的最小正值是![]() ,
,
此时,![]() ,
,
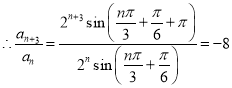
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
……..
![]()
![]()
(3)必要性:若![]() 为等比数列,则
为等比数列,则![]() ,
,
对一切![]() 成立,显然对
成立,显然对![]() 成立.
成立.
![]() 既为2级等比数列,
既为2级等比数列,![]() 也为3级等比数列.
也为3级等比数列.
充分性:若![]() 为2级等比数列,
为2级等比数列,![]() ,则
,则![]() ,
,![]() 均成等比数列,
均成等比数列,
设等比数列![]() ,
,![]() 的公比分别为
的公比分别为![]() ,
,
![]() 为3级等比数列,
为3级等比数列,![]() ,则
,则![]() 成等比数列,设公比为
成等比数列,设公比为![]()
![]() 既是
既是![]() 中的项,也是
中的项,也是![]() 中的项,
中的项,
![]() ,
,![]() 既是
既是![]() 中的项,也是
中的项,也是![]() 中的项,
中的项,![]()
![]() ,
,
![]() ,
,
设![]() ,则
,则![]()
![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
综合得:![]() ,显然
,显然![]() 为等比数列.
为等比数列.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目