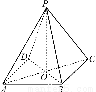
题目内容
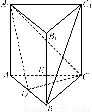
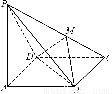
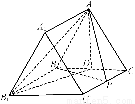
P为△ABC所在平面外一点，O为P在平面ABC内的射影．
(1)若P到△ABC三边距离相等，且O在△ABC的内部，则O是△ABC的________心；
(2)若PA⊥BC，PB⊥AC，则O是△ABC的________心；
(3)若PA，PB，PC与底面所成的角相等，则O是△ABC的________心．
(1)内(2)垂(3)外
【解析】(1)P到△ABC三边距离相等，且O在△ABC的内部，可知O到△ABC三边距离相等，即O是△ABC的内心；(2)由PO⊥平面ABC且BC平面ABC，得PO⊥BC，又PA⊥BC，PO与PA是平面POA内两条相交直线，所以BC⊥平面POA，从而BC⊥AO.同理AC⊥BO，所以O是△ABC的垂心；由PA、PB、PC与底面所成的角相等，易得Rt△POA≌Rt△POB≌Rt△POC，从而OA＝OB＝OC，所以O是△ABC的外心．
练习册系列答案
阅读快车系列答案
相关题目
